LSA,pLSA原理及其代码实现
一. LSA
1. LSA原理
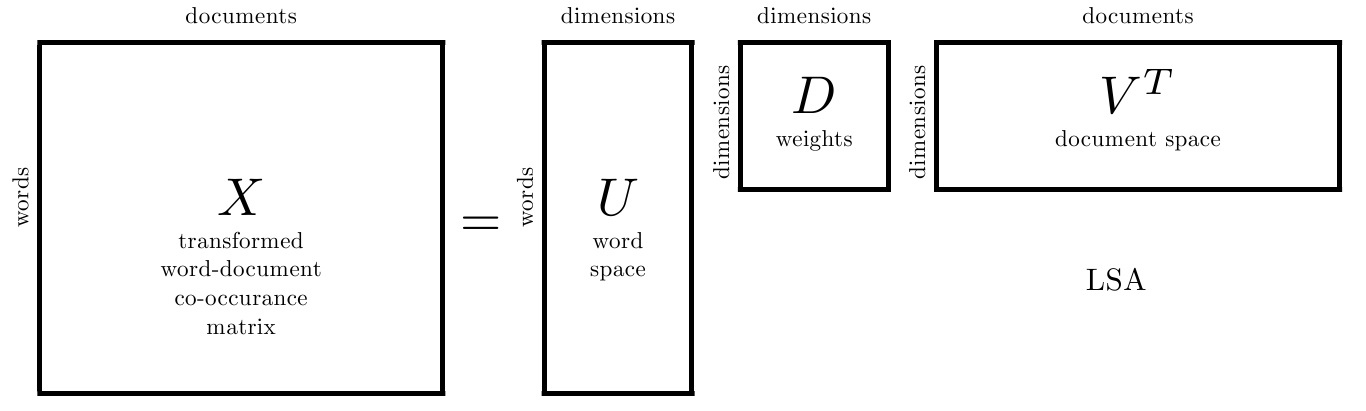
2. LSA的优点
3. LSA的缺点
二. pLSA
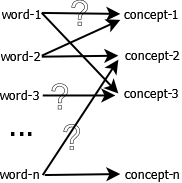
pLSA的建模思路分为两种。
1. 第一种思路
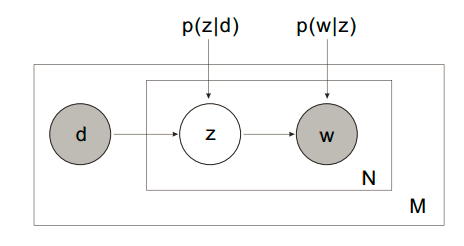
以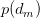 的概率从文档集合
的概率从文档集合 中选择一个文档
中选择一个文档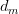
以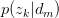 的概率从主题集合
的概率从主题集合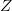 中选择一个主题
中选择一个主题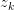
以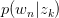 的概率从词集
的概率从词集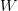 中选择一个词
中选择一个词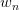
有几点说明:
- 以上变量有两种状态:observed (
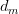 &
&  ) 和 latent (
) 和 latent (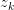 )
)  来自文档,但同时是集合(元素不重复),相当于一个词汇表
来自文档,但同时是集合(元素不重复),相当于一个词汇表
直接的,针对observed variables做建立likelihood function:
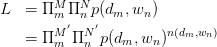
其中,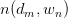 为
为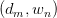 pair出现的次数。为加以区分,之后使用
pair出现的次数。为加以区分,之后使用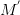 与
与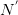 标识对应文档与词汇数量。两边取
标识对应文档与词汇数量。两边取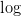 ,得:
,得:
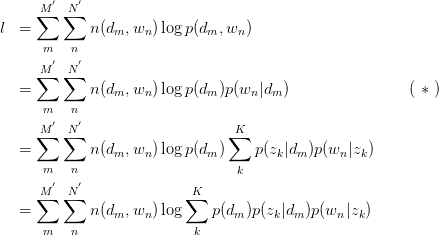
其中,倒数第二步旨在将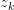 暴露出来。由于likelihood function中
暴露出来。由于likelihood function中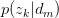 与
与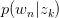 存在latent variable,难以直接使用MLE求解,很自然想到用E-M算法求解。E-M算法主要分为Expectation与Maximization两步。
存在latent variable,难以直接使用MLE求解,很自然想到用E-M算法求解。E-M算法主要分为Expectation与Maximization两步。
假设已知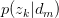 与
与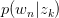 ,求latent variable
,求latent variable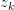 的后验概率
的后验概率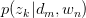
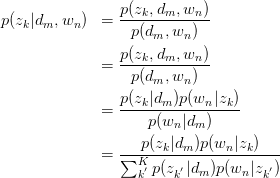
Step 2: Maximization
求关于参数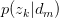 和
和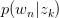 的Complete data对数似然函数期望的极大值,得到最优解。带入E步迭代循环。
的Complete data对数似然函数期望的极大值,得到最优解。带入E步迭代循环。
由 式可得:
式可得:
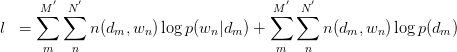
此式后部分为常量。故令:
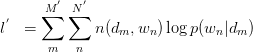
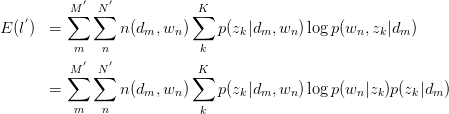
建立以下目标函数与约束条件:
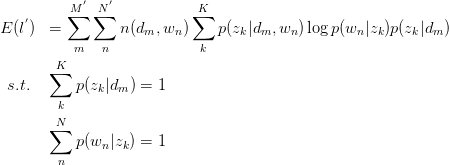
只有等式约束,使用Lagrange乘子法解决:
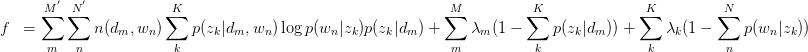
对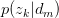 与
与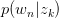 求驻点,得:
求驻点,得:
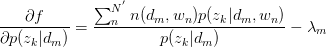
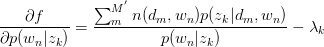
令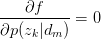 ,得:
,得:
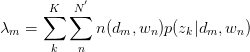 ,故有:
,故有:
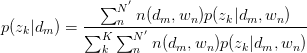
同理,有:
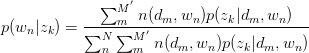
将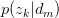 与
与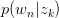 回代Expectation:
回代Expectation:
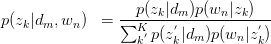 ,循环迭代。
,循环迭代。
pLSA的建模思想较为简单,对于observed variables建立likelihood function,将latent variable暴露出来,并使用E-M算法求解。其中M步的标准做法是引入Lagrange乘子求解后回代到E步。
总结一下使用EM算法求解pLSA的基本实现方法:
2. 第二种思路
这个思路和上面思路的区别就在于对P(d,w)的展开公式使用的不同,思路二使用的是3个概率来展开的,如下:
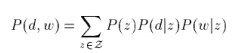
这样子我们后面的EM算法的大致思路都是相同的,就是表达形式变化了,最后得到的EM步骤的更新公式也变化了。当然,思路二得到的是3个参数的更新公式。如下:

你会发现,其实多了一个参数是P(z),参数P(d|z)变化了(之前是P(z|d)),然后P(w|z)是不变的,计算公式也相同。
给定一个文档d,我们可以将其分类到一些主题词类别下。
PLSA算法可以通过训练样本的学习得到三个概率,而对于一个测试样本,其中P(w|z)概率是不变的,但是P(z)和P(d|z)都是需要重新更新的,我们也可以使用上面的EM算法,假如测试样本d的数据,我们可以得到新学习的P(z)和P(d|z)参数。这样我们就可以计算:
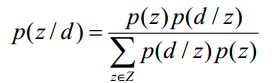
为什么要计算P(z|d)呢?因为给定了一个测试样本d,要判断它是属于那些主题的,我们就需要计算P(z|d),就是给定d,其在主题z下成立的概率是多少,不就是要计算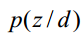 吗。这样我们就可以计算文档d在所有主题下的概率了。
吗。这样我们就可以计算文档d在所有主题下的概率了。
这样既可以把一个测试文档划归到一个主题下,也可以给训练文档打上主题的标记,因为我们也是可以计算训练文档它们的的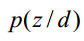 。如果从这个应用思路来说,思路一说似乎更加直接,因为其直接计算出来了
。如果从这个应用思路来说,思路一说似乎更加直接,因为其直接计算出来了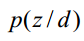 。
。
3. pLSA的优势
4. pLSA的不足
三. pLSA的Python代码实现
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
class Preprocess:
def __init__(self, fname, fsw):
self.fname = fname
# doc info
self.docs = []
self.doc_size = 0
# stop word info
self.sws = []
# word info
self.w2id = {}
self.id2w = {}
self.w_size = 0
# stop word list init
with open(fsw, 'r') as f:
for line in f:
self.sws.append(line.strip())
def __work(self):
with open(self.fname, 'r') as f:
for line in f:
line_strip = line.strip()
self.doc_size += 1
self.docs.append(line_strip)
items = line_strip.split()
for it in items:
if it not in self.sws:
if it not in self.w2id:
self.w2id[it] = self.w_size
self.id2w[self.w_size] = it
self.w_size += 1
self.w_d = np.zeros([self.w_size, self.doc_size], dtype=np.int)
for did, doc in enumerate(self.docs):
ws = doc.split()
for w in ws:
if w in self.w2id:
self.w_d[self.w2id[w]][did] += 1
def get_w_d(self):
self.__work()
return self.w_d
def get_word(self, wid):
return self.id2w[wid]
if __name__ == '__main__':
fname = './data.txt'
fsw = './stopwords.txt'
pp = Preprocess(fname, fsw)
2. plsa.py
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
import time
import logging
def normalize(vec):
s = sum(vec)
for i in range(len(vec)):
vec[i] = vec[i] * 1.0 / s
def llhood(w_d, p_z, p_w_z, p_d_z):
V, D = w_d.shape
ret = 0.0
for w, d in zip(*w_d.nonzero()):
p_d_w = np.sum(p_z * p_w_z[w,:] * p_d_z[d,:])
if p_d_w > 0:
ret += w_d[w][d] * np.log(p_d_w)
return ret
class PLSA:
def __init__(self):
pass
def train(self, w_d, Z, eps):
V, D = w_d.shape
# create prob array, p(d|z), p(w|z), p(z)
p_d_z = np.zeros([D, Z], dtype=np.float)
p_w_z = np.zeros([D, Z], dtype=np.float)
p_z = np.zeros([Z], dtype=np.float)
# initialize
p_d_z = np.random.random([D, Z])
for d_idx in range(D):
normalize(p_d_z[d_idx])
p_w_z = np.random.random([V, Z])
for w_idx in range(V):
normalize(p_w_z[w_idx])
p_z = np.random.random([Z])
normalize(p_z)
# iteration until converge
step = 1
pp_d_z = p_d_z.copy()
pp_w_z = p_w_z.copy()
pp_z = p_z.copy()
while True:
logging.info('[ iteration ] step %d' % step)
step += 1
p_d_z *= 0.0
p_w_z *= 0.0
p_z *= 0.0
# run EM algorithm
for w_idx, d_idx in zip(*w_d.nonzero()):
#print '[ EM ] >>>>>> E step : '
p_z_d_w = pp_z * pp_d_z[d_idx,:] * pp_w_z[w_idx,:]
normalize(p_z_d_w)
#print '[ EM ] >>>>>> M step : '
tt = w_d[w_idx, d_idx] * p_z_d_w
p_w_z[w_idx,:] += tt
p_d_z[d_idx,:] += tt
p_z += tt
normalize(p_w_z)
normalize(p_d_z)
p_z = p_z / w_d.sum()
# check converge
l1 = llhood(w_d, pp_z, pp_w_z, pp_d_z)
l2 = llhood(w_d, p_z, p_w_z, p_d_z)
diff = l2 - l1
logging.info('[ iteration ] l2-l1 %.3f - %.3f = %.3f ' % (l2, l1, diff))
if abs(diff) < eps:
logging.info('[ iteration ] End EM ')
return (l2, p_d_z, p_w_z, p_z)
pp_d_z = p_d_z.copy()
pp_w_z = p_w_z.copy()
pp_z = p_z.copy()
3. main.py
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from preprocess import Preprocess as PP
from plsa import PLSA
import numpy as np
import logging
import time
def main():
# setup logging --------------------------
logging.basicConfig(filename='plsa.log',
level=logging.INFO,
format='%(asctime)s %(filename)s[line:%(lineno)d] %(levelname)s %(message)s',
datefmt='%a, %d %b %Y %H:%M:%S')
#console = logging.StreamHandler()
#console.setLevel(logging.INFO)
#logging.getLogger('').addHandler(console)
# some basic configuration ---------------
fname = './data.txt'
fsw = './stopwords.txt'
eps = 20.0
key_word_size = 10
# preprocess -----------------------------
pp = PP(fname, fsw)
w_d = pp.get_w_d()
V, D = w_d.shape
logging.info('V = %d, D = %d' % (V, D))
# train model and get result -------------
pmodel = PLSA()
for z in range(3, (D+1), 10):
t1 = time.clock()
(l, p_d_z, p_w_z, p_z) = pmodel.train(w_d, z, eps)
t2 = time.clock()
logging.info('z = %d, eps = %f, time = %f' % (z, l, t2-t1))
for itz in range(z):
logging.info('Topic %d' % itz)
data = [(p_w_z[i][itz], i) for i in range(len(p_w_z[:,itz]))]
data.sort(key=lambda tup:tup[0], reverse=True)
for i in range(key_word_size):
logging.info('%s : %.6f ' % (pp.get_word(data[i][1]), data[i][0]))
if __name__ == '__main__':
main()
版权声明:
本文由笨兔勿应所有,发布于http://www.cnblogs.com/bentuwuying。如果转载,请注明出处,在未经作者同意下将本文用于商业用途,将追究其法律责任。
LSA,pLSA原理及其代码实现的更多相关文章
- flume原理及代码实现
转载标明出处:http://www.cnblogs.com/adealjason/p/6240122.html 最近想玩一下流计算,先看了flume的实现原理及源码 源码可以去apache 官网下载 ...
- Java Base64加密、解密原理Java代码
Java Base64加密.解密原理Java代码 转自:http://blog.csdn.net/songylwq/article/details/7578905 Base64是什么: Base64是 ...
- Base64加密解密原理以及代码实现(VC++)
Base64加密解密原理以及代码实现 转自:http://blog.csdn.net/jacky_dai/article/details/4698461 1. Base64使用A--Z,a--z,0- ...
- AC-BM算法原理与代码实现(模式匹配)
AC-BM算法原理与代码实现(模式匹配) AC-BM算法将待匹配的字符串集合转换为一个类似于Aho-Corasick算法的树状有限状态自动机,但构建时不是基于字符串的后缀而是前缀.匹配 时,采取自后向 ...
- Java基础知识强化之集合框架笔记47:Set集合之TreeSet保证元素唯一性和比较器排序的原理及代码实现(比较器排序:Comparator)
1. 比较器排序(定制排序) 前面我们说到的TreeSet的自然排序是根据集合元素的大小,TreeSet将它们以升序排列. 但是如果需要实现定制排序,比如实现降序排序,则要通过比较器排序(定制排序)实 ...
- PHP网站安装程序的原理及代码
原文:PHP网站安装程序的原理及代码 原理: 其实PHP程序的安装原理无非就是将数据库结构和内容导入到相应的数据库中,从这个过程中重新配置连接数据库的参数和文件,为了保证不被别人恶意使用安装文件,当安 ...
- 免费的Lucene 原理与代码分析完整版下载
Lucene是一个基于Java的高效的全文检索库.那么什么是全文检索,为什么需要全文检索?目前人们生活中出现的数据总的来说分为两类:结构化数据和非结构化数据.很容易理解,结构化数据是有固定格式和结构的 ...
- 机器学习之KNN原理与代码实现
KNN原理与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9670187.html 1. KNN原理 K ...
- 机器学习之AdaBoost原理与代码实现
AdaBoost原理与代码实现 本文系作者原创,转载请注明出处: https://www.cnblogs.com/further-further-further/p/9642899.html 基本思路 ...
随机推荐
- Server Tomcat v6.0 Server at localhost was unable to start within 45 seconds问题
错误:Server Tomcat v6.0 Server at localhost was unable to start within 45 seconds. If the server requi ...
- mysql获取所有分类的前n条记录的两种方法浅析
项目中有个需求是获取出展会分类下的前n条展商. 刚开始的思路是用group by 获取出展会的分类,后面再根据分类获取该分类下的n个展商,但也需要第一次获取出展会的时候也获取所有的每个展会分类下的 ...
- Android学习地址
Google Android官方培训课程中文版http://hukai.me/android-training-course-in-chinese/
- java-android推送
之前做的推送,考虑了很多,最后因为各个因素,选择了极光的.
- centos7.2 默认启动内核修改
总所周知,修改centos6的内核启动顺序,只需要修改/etc/grub.conf 里的default项配置即可.那么centos7系统该如何修改呢? 下面就centos7系统修改内核,做如下记录: ...
- MySql学习(MariaDb)
资料 http://www.cnblogs.com/lyhabc/p/3691555.html http://www.cnblogs.com/lyhabc/p/3691555.html MariaDb ...
- Task:取消异步计算限制操作 & 捕获任务中的异常
Why:ThreadPool没有内建机制标记当前线程在什么时候完成,也没有机制在操作完成时获得返回值,因而推出了Task,更精确的管理异步线程. How:通过构造方法的参数TaskCreationOp ...
- git/ssh捋不清的几个问题
主要是 windows 用户会遇到很多纠结的问题,linux/unix 用户属于这方面的高端用户,应该有能力处理此类问题,而且网络上也有很多解决方案,本文的授众是 windows 用户.由于今天配置了 ...
- Word文档合并的一种实现
今天遇到一个问题,就是需要把多个Word文档的内容追加到一个目标Word文档的后面,如果我有目标文档a.doc以及其他很多个文档b.doc,c.doc…等等数量很多.这个问题,如果是在服务端的话,直接 ...
- 一个老菜鸟所理解的UX及产品流
从事前端开发到目前为止已经有4年多的时间了,从一个小菜鸟一路依靠自学,到目前总算一个老菜鸟了.当然了,从事前端的工作,是免不了要对产品以及用户体验有些许了解的.最近谈论起这方面的内容,就按照自己的想法 ...
