Linear Algebra lecture3 note
Matrix multiplication(4 ways!)
Inverse of A
Gauss-Jordan / find inverse of A
Matrix multiplication
1、点积法
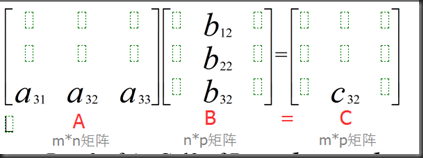
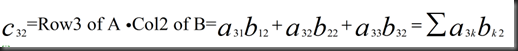
2、matrix * column=comb of columns
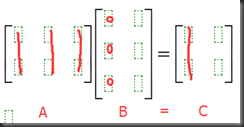
columns of C are comb of cols of A
3、matrix * row = comb of rows
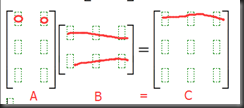
rows of C are comb of rows of B
4、matrix * matrix=comb of row*col
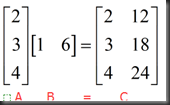
AB=sum of (cols of A )*(rows of B)
another example:
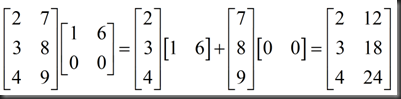
*5、Block (分块行 * 分块列)
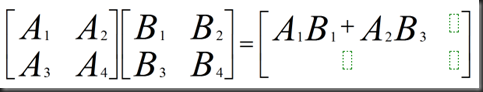
Inverses( Square matrices)
if inverse of A exits, then
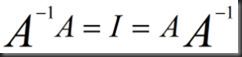
invertible, non-singular
思考如何求此矩阵的逆,矩阵及其逆应满足条件:
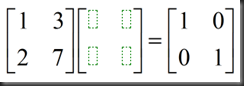
设逆矩阵由元素a,b,c,d构成,如图:
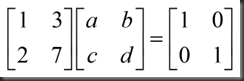
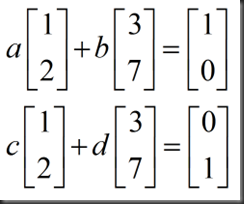
以上讨论的都是逆矩阵存在的情况,下面举例讨论逆矩阵不存在的情况(singular case,no inverse),
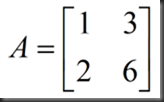
可以从以下三方面来解释:
1、行列式为0
2、假设A`存在,A中两列向量共线,所以不可能通过线性组合构成单位矩阵,AA`≠I,就没有A`的说法了
3、You can find a vector X with AX=0 (X≠0)
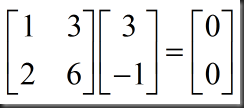
由于AX=0,假设A`存在,等式两边同时乘以A`,A`AX=A`0=0, IX=0,X=0 与 X≠0矛盾,故假设不成立
若矩阵中其中一列对线性组合毫无贡献,则矩阵不可能有逆
Gauss Jordan(solve 2 equations at once)
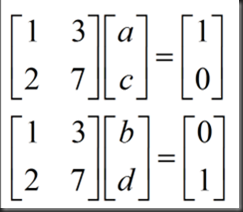
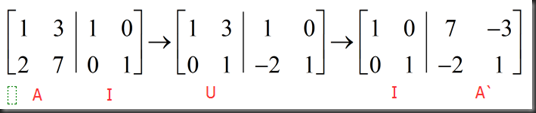
可得到A的逆矩阵形式为:

解释推导:
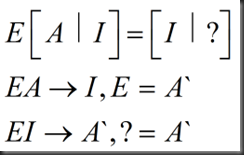
Linear Algebra lecture3 note的更多相关文章
- Linear Algebra lecture1 note
Professor: Gilbert Strang Text: Introduction to Linear Algebra http://web.mit.edu/18.06 Lecture 1 ...
- Linear Algebra lecture9 note
Linear independence Spanning a space Basis and dimension 以上概念都是针对a bunch of vectors, 不是矩阵里的概念 Supp ...
- Linear Algebra lecture10 note
Four fundamental subspaces( for matrix A) if A is m by n matrix: Column space C(A) in Rm (列空间在m维实 ...
- Linear Algebra lecture8 note
Compute solution of AX=b (X=Xp+Xn) rank r r=m solutions exist r=n solutions unique example: 若想方程有解 ...
- Linear Algebra lecture7 note
Computing the nullspace (Ax=0) Pivot variables-free variables Special solutions: rref( A)=R rank o ...
- Linear Algebra lecture6 note
Vector spaces and subspaces Column space of A solving Ax=b Null space of A Vector space requiremen ...
- Linear Algebra Lecture5 note
Section 2.7 PA=LU and Section 3.1 Vector Spaces and Subspaces Transpose(转置) example: 特殊情况,对称 ...
- Linear Algebra lecture4 note
Inverse of AB,A^(A的转置) Product of elimination matrices A=LU (no row exchanges) Inverse of AB,A^(A ...
- Codeforces Gym101502 B.Linear Algebra Test-STL(map)
B. Linear Algebra Test time limit per test 3.0 s memory limit per test 256 MB input standard input ...
随机推荐
- 在linux中查询硬件相关信息
1.查询cpu的相关 a.查询CPU的统计信息 使用命令:lscpu 得到的结果如下: Architecture: x86_64 CPU op-mode(s): -bit, -bit Byte Ord ...
- The guard was taken to hospital in a critical condition.
The Prince George's County Fire Department said the guard was taken to hospital in a critical condit ...
- 安装了简易版XP系统后不能安装IIS的解决办法
第一步 找到C:\WINDOWS\inf文件夹中的sysoc.inf文件,在 [Components]区域中的NetOC=netoc.dll,NetOcSetupProc,netoc.inf,,7和c ...
- 解决ie6 fixed 定位以及抖动问题
像你所遇到的问题一样, IE6浏览器有太多的bug让制作网页的人头疼.这篇文章介绍的是介绍的是如何解决IE6不支持position:fixed;属性的办法.如果我们需要做某个元素始终位于浏览器的底部, ...
- linux下内存泄露检测工具Valgrind介绍
目前在linux开发一个分析实时路况的应用程序,在联合测试中发现程序存在内存泄露的情况. 这下着急了,马上就要上线了,还好发现了一款Valgrind工具,完美的解决了内存泄露的问题. 推荐大家可以使用 ...
- docker 源码分析 三(基于1.8.2版本),NewDaemon启动
本文来分析一下New Daemon的启动过程:在daemon/daemon.go文件中: func NewDaemon(config *Config, registryService *registr ...
- 2016 - 3 - 12 SQLite的学习之SQL语言入门
1.SQL语句的特点: 1.1 不区分大小写 1.2 每条语句以;结尾 2.SQL语句中常用关键字: select,insert,update,from,create,where,desc,order ...
- 估计PI——OpenCV&Cpp
来源:<Learning Image Processing With OpenCV> 算法原理:蒙特卡洛 PI的计算公式: Cpp代码: #include <opencv2/open ...
- win7 32 bit VS2012 OpenCV3.0配置
今天看CPP基础,想起来之前在vs2012配置opencv3未成功,就忍不住再次配置一... 环境:win7 32bit vs2012 opencv3.0 主要参考这几篇博文:1,2,3 上面的博文已 ...
- Oracle设置自动递增的方法
1)创建序列: create sequence SEQ_TEST --字段名 minvalue 1 --最小值 maxvalue XXXXX --设置最大值 start wit ...
