KNN近邻算法

K近邻(KNN，k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻，就是k个最近的邻居的意思，说的是每个样本都可以用它最接近的k个邻居来代表。kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时，只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，kNN方法较其他方法更为适合。

-- 邻近算法 百度百科

KNN近邻算法思想

根据上文 K-means 算法分类，可以将一堆 毫无次序 的样本分成N个簇，如下：

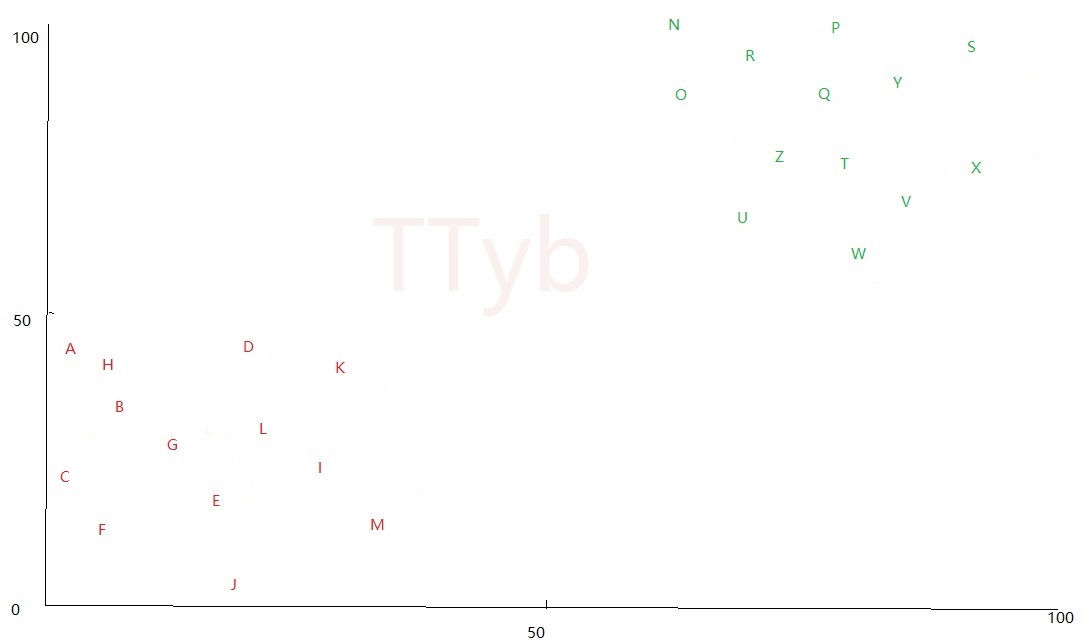
上图中红色代表一个分簇，绿色代表另一个分簇，这两个簇现在可以称呼为 训练样本 ，现在突然出现了一个 黄色的四边形 ，如下：

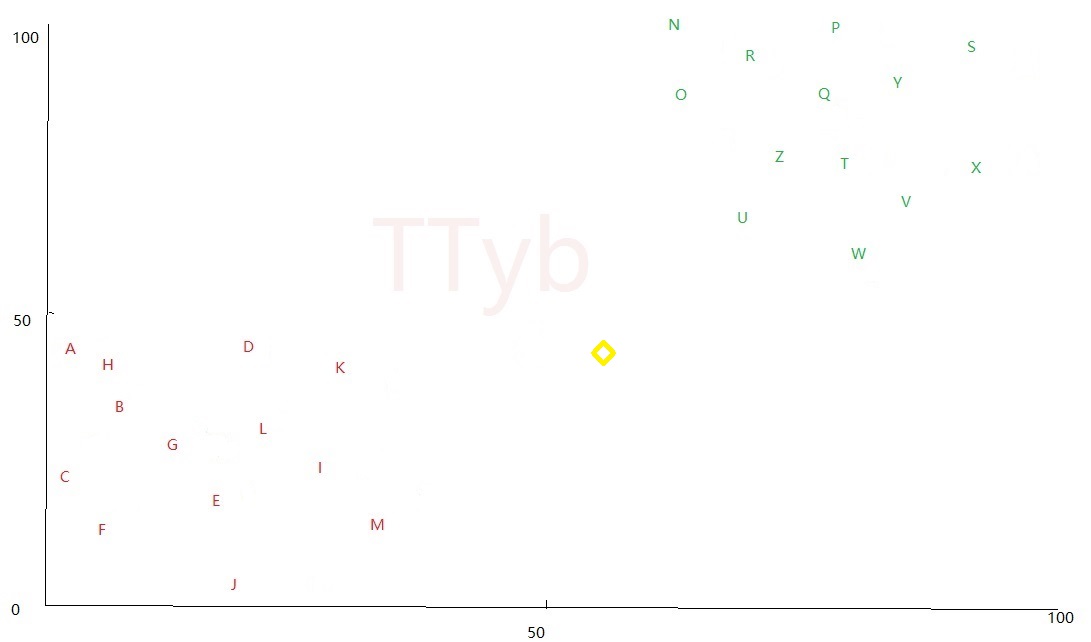
该 黄色的四边形 现在还不知道属于哪一个分簇。选取 黄色的四边形 周围的 K个点 (K一定要是奇数)：

1. 当K=3时，直观看出 黄色的四边形 周围的3个点为：K、M、U，就可以判断 黄色的四边形 属于红色簇
2. 当K=4时，直观看出 黄色的四边形 周围的3个点为：K、M、U、W，无法判断 黄色的四边形 属于哪个簇，因此不能为偶数
3. 当K=5时，直观看出 黄色的四边形 周围的3个点为：K、M、U、W、Z，就可以判断 黄色的四边形 属于绿色簇

KNN近邻算法就是以一定量的训练样本，来对其他未知样本进行分类，分类的标准和选取的K值有很大关系

KNN近邻算法实现

假设训练样本为：

clusters = {
    'cluster2': {'H': {'y': 25, 'x': 27}, 'F': {'y': 30, 'x': 36}, 'G': {'y': 14, 'x': 31}, 'A': {'y': 34, 'x': 24},
                 'D': {'y': 33, 'x': 25}, 'I': {'y': 11, 'x': 28}, 'C': {'y': 23, 'x': 26}, 'E': {'y': 23, 'x': 38},
                 'B': {'y': 23, 'x': 6}, 'L': {'y': 15, 'x': 7}, 'K': {'y': 25, 'x': 17}, 'M': {'y': 39, 'x': 24},
                 'J': {'y': 26, 'x': 21}},
    'cluster1': {'R': {'y': 97, 'x': 80}, 'N': {'y': 82, 'x': 99}, 'U': {'y': 81, 'x': 95}, 'V': {'y': 88, 'x': 79},
                 'O': {'y': 85, 'x': 73}, 'Y': {'y': 99, 'x': 87}, 'X': {'y': 72, 'x': 88},
                 'Q': {'y': 84, 'x': 100}, 'T': {'y': 70, 'x': 84}, 'W': {'y': 100, 'x': 89},
                 'S': {'y': 67, 'x': 86}, 'Z': {'y': 97, 'x': 66}, 'P': {'y': 88, 'x': 62}}}

随机生成一个point：

# 随机生成一个点
def buildpoint():
    temp = {}
    x = random.randint(0, 100)
    y = random.randint(0, 100)

    temp["x"] = x
    temp["y"] = y
    return temp

分别计算计算这个point与26个字母的 欧氏距离

# 取得point与K个值的距离
def classify(K, clusters, point):
    dict = {}
    distan = {}
    for cluster in clusters:
        for key in clusters[cluster].keys():
            distan[key] = distance(clusters[cluster][key]["x"], point["x"], clusters[cluster][key]["y"], point["y"])

    # reverse=False值按照从小到大排序
    distan = sorted(distan.items(), key=lambda d: d[1], reverse=False)
    for i in range(K):
        key = distan[i][0]
        value = distan[i][1]
        dict[key] = value

    return dict

返回的距离 distan 为：

# [('E', 21.02379604162864), ('F', 21.095023109728988), ('H', 30.805843601498726), ('G', 31.622776601683793), ('D', 32.01562118716424), ('C', 32.28002478313795), ('A', 33.06055050963308), ('M', 33.734255586866), ('I', 35.805027579936315), ('J', 36.49657518178932), ('K', 40.607881008493905), ('S', 45.45327270945405), ('T', 46.61544808322666), ('X', 50.60632371551998), ('B', 51.78802950489621), ('L', 52.81098370604357), ('O', 55.362442142665635), ('P', 56.22277118748239), ('V', 60.166435825965294), ('U', 62.00806399170998), ('N', 65.29931086925804), ('Z', 65.62011886609167), ('Q', 67.47592163134935), ('R', 68.9492567037528), ('Y', 73.40980860893181), ('W', 75.15317691222374)]

因为本文选取的 K=3 ,所以返回了距离point最近的3个点：

# {'U': 30.805843601498726, 'M': 21.02379604162864, 'K': 21.095023109728988}

最后判断这3个点属于哪个分簇即可：

def judgecluster(dict, clusters):
    newdict = {}
    for cluster in clusters:
        for key in dict.keys():
            if key in clusters[cluster]:
                if cluster in newdict:
                    newdict[cluster] += 1
                else:
                    newdict[cluster] = 1

    newdict = sorted(newdict.items(), key=lambda d: d[1], reverse=True)
    print("Point属于分簇" + str(newdict[0][0]))
    print(newdict)

    return newdict

返回的结果为：

# [('cluster2', 2), ('cluster1', 1)]
Point属于分簇cluster2

源码在我的博客上面：

TTyb