Subsets I&&II——经典题

Subsets I

Given a set of distinct integers, nums, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If nums = [1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

思路一(http://www.cnblogs.com/felixfang/p/3775712.html)

可以用递推的思想，观察S=[], S =[1], S = [1, 2] 时解的变化。

可以发现S=[1, 2] 的解就是 把S = [1]的所有解末尾添上2，然后再并上S = [1]里面的原有解。因此可以定义vector<vector<int> > 作为返回结果res, 开始时res里什么都没有，第一步放入一个空的vecotr<int>，然后这样迭代n次，每次更新res 内容，最后返回res。

代码：

class Solution {
public:
    vector<vector<int> > subsets(vector<int> &S) {
        vector<vector<int> > res;
        vector<int> emp;
        res.push_back(emp);
        sort(S.begin(), S.end());
        if(S.size() == ) return res;
        for(vector<int>::iterator ind = S.begin(); ind < S.end(); ++ind){
            int size = res.size();
            for(int i = ; i < size; ++i){
                vector<int> v;
                for(vector<int>::iterator j = res[i].begin(); j < res[i].end(); ++j){
                   v.push_back(*j);
                }
                v.push_back(*ind);
                res.push_back(v);
            }
        }
        return res;
    }
};

思路二

所谓子集，就是包含原集合中的一些元素，不包含另一些元素。如果单独看某一个元素，它都有两种选择："被包含在子集中"和"不被包含在子集中"，对于元素个数为n、且不含重复元素的S，子集总数是2ⁿ。因此我们可以遍历S的所有元素，然后用递归考虑每一个元素包含和不包含的两种情况。

代码，这种思路需要用到递归

（代码来自http://www.acmerblog.com/leetcode-solution-subsets-6227.html 这篇博客可以好好看看）

// LeetCode, Subsets
 
// 增量构造法，深搜，时间复杂度O(2^n)，空间复杂度O(n)
 
class Solution {
public:
    vector<vector<int> > subsets(vector<int> &S) {
        sort(S.begin(), S.end());  // 输出要求有序
        vector<vector<int> > result;
        vector<int> path;
        subsets(S, path, , result);
        return result;
    }
 
private:
    static void subsets(const vector<int> &S, vector<int> &path, int step,
            vector<vector<int> > &result) {
        if (step == S.size()) {
            result.push_back(path);
            return;
        }
        // 不选S[step]
        subsets(S, path, step + , result);
        // 选S[step]
        path.push_back(S[step]);
        subsets(S, path, step + , result);
        path.pop_back();
    }
};

思路同上，代码中可以采用位向量法，开一个位向量bool selected[n]，每个元素可以选或者不选。

// LeetCode, Subsets
// 位向量法，深搜，时间复杂度O(2^n)，空间复杂度O(n)
class Solution {
public:
    vector<vector<int> > subsets(vector<int> &S) {
        sort(S.begin(), S.end());  // 输出要求有序
        vector<vector<int> > result;
        vector<bool> selected(S.size(), false);
        subsets(S, selected, , result);
        return result;
    }
private:
    static void subsets(const vector<int> &S, vector<bool> &selected, int step,
            vector<vector<int> > &result) {
        if (step == S.size()) {
            vector<int> subset;
            for (int i = ; i < S.size(); i++) {
                if (selected[i]) subset.push_back(S[i]);
            }
            result.push_back(subset);
            return;
        }
        // 不选S[step]
        selected[step] = false;
        subsets(S, selected, step + , result);
        // 选S[step]
        selected[step] = true;
        subsets(S, selected, step + , result);
    }
};

Subsets II

Given a collection of integers that might contain duplicates, nums, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If nums = [1,2,2], a solution is:

[

[2],

[1],

[1,2,2],

[2,2],

[1,2],

[]

]

思路一：

其实比较简单，就是每当遇到重复元素的时候我们就只把当前结果集的后半部分加上当前元素加入到结果集中，因为后半部分就是上一步中加入这个元素的所有子集，上一步这个元素已经加入过了，前半部分如果再加就会出现重复。所以算法上复杂度上没有提高，反而少了一些操作，就是遇到重复时少做一半，不过这里要对元素集合先排序，否则不好判断重复元素。同样的还是可以用递归和非递归来解，不过对于重复元素的处理是一样的。

我们以S=[1,2,2]为例:

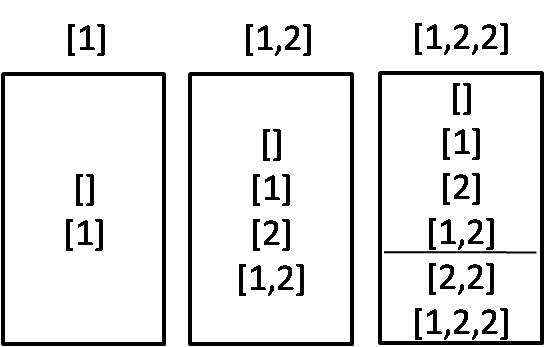
可以发现从S=[1,2]变化到S=[1,2,2]时，多出来的有两个子集[2,2]和[1,2,2]，这两个子集，其实就是 [2], [1,2]末尾都加上2 而产生。而[2], [1,2] 这两个子集实际上是 S=[1,2]的解到 S=[1]的解 新添加的部分。

因此，若S中有重复元素，可以先排序；遍历过程中如果发现当前元素S[i] 和 S[i-1] 相同，那么不同于原有思路中“将当前res中所有自己拷贝一份再在末尾添加S[i]”的做法，我们只将res中上一次添加进来的子集拷贝一份，末尾添加S[i]。

class Solution {
public:
    vector<vector<int> > subsetsWithDup(vector<int> &S) {
        vector<vector<int> > subsets;
        vector<int> v;
        subsets.push_back(v);
        if(S.empty()) return subsets;
        sort(S.begin(), S.end());
        int m = 0; //m 用来存储上一次加进来的子集们的起始index
        for(vector<int>::iterator i = S.begin(); i < S.end(); ++i){
            int start = ((i != S.begin() && *i == *(i-1)) ? m : 0); //如果S的当前元素和前一个元素相同，只拷贝上次加进来的子集
            int end = subsets.size();
            for(int j = start; j < end; ++j){
                vector<int> vt;
                for(vector<int>::iterator k = subsets[j].begin(); k < subsets[j].end(); ++k){
                    vt.push_back(*k);
                }
                vt.push_back(*i);
                subsets.push_back(vt);
            }
            m = end;
        }
        return subsets;
    }
};

思路二：

对于含有重复元素的S，可以先排序，然后考虑去重：我们可以发现如果所遍历的当前元素S[i] 和 目前的子集的末尾元素相同，那么就不再需要考虑"不包含当前元素到子集中"的情况，只需要考虑"包含当前元素到子集中一种情况"。举个例子：对于S=[1,2,2]，如果遍历到第二个"2"，当前子集v是[1, 2]，这个时候如果考虑"不把2包含进子集的情况"，即维持子集=[1,2]不动，遍历下一个元素；这样其结果会出现重复。因为考虑另一个递归调用，其当前子集v是[1]，也遍历到了S的第二个"2"，它将这个"2"元素放入当前子集，虽然继续遍历下一个元素。这两个递归调用的结果是重复的。因此，若当前递归调用所遍历到的元素和当前子集v的末尾元素相同，只考虑"把当前元素添加到子集末尾"的情况。

// LeetCode, Subsets II
// 增量构造法，版本1，时间复杂度O(2^n)，空间复杂度O(n)
class Solution {
public:
    vector<vector<int> > subsetsWithDup(vector<int> &S) {
        sort(S.begin(), S.end());  // 必须排序
        vector<vector<int> > result;
        vector<int> path;
        dfs(S, S.begin(), path, result);
        return result;
    }
private:
    static void dfs(const vector<int> &S, vector<int>::iterator start,
            vector<int> &path, vector<vector<int> > &result) {
        result.push_back(path);
        for (auto i = start; i < S.end(); i++) {
            if (i != start && *i == *(i-)) continue;
            path.push_back(*i);
            dfs(S, i + , path, result);
            path.pop_back();
        }
    }
};