[TCO2013]LitPanels

题意：一个$n\times m$的无色网格，你可以在其中选择两个$x\times y$的子矩形并在其中将其中任意的格子涂上颜色，问最终能得到多少种不同的网格

做这题会用到一个概念叫包围盒（bounding box），一组平面图形的包围盒就是包含它的最小矩形，在本题中，我们限制包围盒的边界与网格平行，对每种大小的包围盒计算有多少种图案满足要求

对于一个大小固定的包围盒，有两个限制：1.包围盒的$4$个边界上都必须有至少一个点被涂色，2.选择的两个矩形要么一个在包围盒的左上，另一个在右下，要么一个在右上，另一个在左下

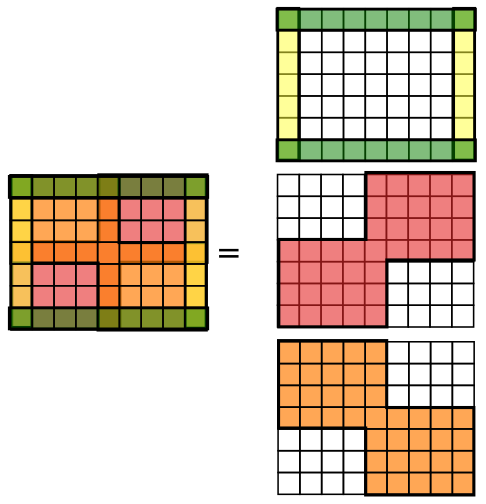
对应到题解中的这张图，第二个限制就是：红色和橙色区域中不能同时有被涂色的格子

于是我们有了$6$个区域：$4$个边界和剩下两个在被选矩形之外的区域，考虑用状压表示占用区域的状态

先预处理$c_i$表示状态为$i$的格子有多少个，然后设$f_{i,j}$表示考虑了$1\cdots i$的状态，已经填了$j$的状态，填剩下格子的方案数

考虑倒推，当$i=64$时$f_{i,j}$表示的是$j$这个状态合不合法，所以$f_{64,2^0+2^1+2^2+2^3}=f_{64,2^0+2^1+2^2+2^3+2^4}=f_{64,2^0+2^1+2^2+2^3+2^5}=1$

然后是转移，对于$f_{i,j}$，如果要填状态为$i$的格子那么有$2^{c_i}-1$种填法，所以$f_{i,j}=f_{i+1,j}+f_{i+1,i|j}(2^{c_i}-1)$

最后的答案即为$f_{0,0}$

算出每个不同大小的包围盒$\times$放置包围盒的方案数，加起来就是答案

#include<stdio.h>
#include<string.h>
typedef long long ll;
const int mod=1000000007;
int mul(int a,int b){return(ll)a*b%mod;}
int ad(int a,int b){return(a+b)%mod;}
void inc(int&a,int b){(a+=b)%=mod;}
int pw[2010],c[70],s[50][50],f[70][70];
int calc(int n,int m,int x,int y){
	int i,j;
	memset(c,0,sizeof(c));
	memset(s,0,sizeof(s));
	memset(f,0,sizeof(f));
	for(i=1;i<=m;i++){
		s[1][i]|=1;
		s[n][i]|=2;
	}
	for(i=1;i<=n;i++){
		s[i][1]|=4;
		s[i][m]|=8;
	}
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++){
			if(!(i<=x&&j<=y)&&!(i>=n-x+1&&j>=m-y+1))s[i][j]|=16;
			if(!(i>=n-x+1&&j<=y)&&!(i<=x&&j>=m-y+1))s[i][j]|=32;
		}
	}
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++)c[s[i][j]]++;
	}
	f[64][15]=f[64][31]=f[64][47]=1;
	for(i=63;i>=0;i--){
		for(j=0;j<64;j++)f[i][j]=ad(f[i+1][j],mul(pw[c[i]]-1,f[i+1][j|i]));
	}
	return f[0][0];
}
class LitPanels{
	public:
		int countPatterns(int n,int m,int x,int y){
			int i,j,s;
			pw[0]=1;
			for(i=1;i<=n*m;i++)pw[i]=mul(pw[i-1],2);
			s=1;
			for(i=1;i<=n;i++){
				for(j=1;j<=m;j++)inc(s,mul(calc(i,j,x,y),mul(n-i+1,m-j+1)));
			}
			return s;
		}
};
/*
int main(){
	int a,b,c,d;
	LitPanels cl;
	scanf("%d%d%d%d",&a,&b,&c,&d);
	printf("%d",cl.countPatterns(a,b,c,d));
}
*/