【jzyzoj】【p1320 patrol】 巡逻（网络流最小割例题）

　　描述 Description

FJ有个农场，其中有n块土地，由m条边连起来。FJ的养牛场在土地1，在土地n有个新开张的雪糕店。Bessie经常偷偷溜到雪糕店，当Bessie去的时候，FJ就要跟上她。但是Bessie很聪明，她在从雪糕店返回时不会经过去雪糕店时经过的农场，因此FJ总是抓不住Bessie。
为了防止Bessie生病，FJ决定把一些诚实的狗放在一些土地(1和n除外)上，使Bessie无法在满足每块土地最多只经过一次的条件的情况下，从养牛场溜到雪糕店然后又溜回养牛场。
求出FJ最少要放多少只狗。数据保证1和n间没有直接的连边。
输入格式 Input Format
* Line 1: Two integers: N and M.

* Lines 2..M+1: Each line contains two integers A and B that describe
　　　　a trail joining fields A and B. It is possible to travel
　　　　along this trail both ways. No trail will appear twice.
输出格式 Output Format
Line 1: A single integer that tells how many fields FJ should guard.
样例输入 Sample Input

6 7
1 2
2 6
1 3
3 4
3 5
4 6
5 6
样例输出 Sample Output

1

OUTPUT DETAILS:

FJ can guard field 2 (for example). FJ could guard both fields 4 and
5, but that would require more dogs.
时间限制 Time Limitation
1s
注释 Hint
数据范围：n<=1000，m<=10000。
来源 Source
usaco

　　不得不说这道题细节要求是非常高的，如果不注意就会WA。。。

　　刚开始建图也建对了，后来想了想，还是不要用

insert(i,i,);

这种奇奇怪怪的自身相连来拆点，于是给i，i+n连边。需要注意的是，源点S,T【此题为1，n】，不需要拆。

　　1.然后问题就来了，建完图有数据是过不去的。经过思考【看数据】，发现是有坑的。因为你的输出是ans-1，所以如果根本没有路去汇点T，那么ans=0，这时候ans-1为-1............所以输出要特判

　　2.第二个坑就是很鬼畜的，，，看如下N=6的对于样例的图【忽略我画的不是双向边】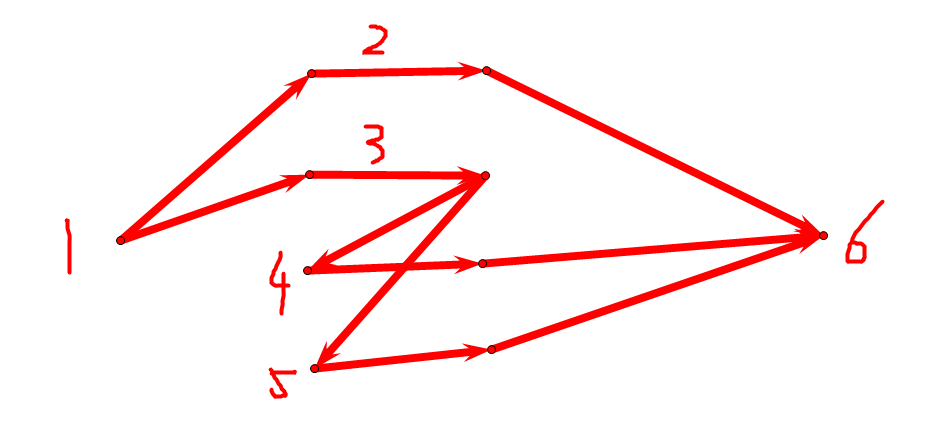

显然进行拆点后，最大流是2，最小割是1。根据此图建图时，对于给出的x，y相连，显然我们

insert(x+n,y,);
insert(y+n,x,);

然而这又是一个坑。如果x=1或者y=1，那么肯定是不需要x+n或y+n的，这里也要特判，才能解决s=1，t=n的答案。

下面是AC代码：

#include<bits/stdc++.h>
#define INF 2100000000
using std::min;
struct qaq
{
    int y,v,nt;
}e[];
int rev[];
int lin[];
int q[];
int level[];
int s,t;
int len=;
int n,m;
int ans=;    

char buf[<<],*fs,*ft;
inline char getc(){ return (fs==ft && (ft=(fs=buf)+fread(buf,,<<,stdin),fs==ft))?:*fs++; }
int read()
{
    char ch=getc();int x=;
    while(!isdigit(ch)) ch=getc();
    while(isdigit(ch)) {x=(x<<)+(x<<)+ch-''; ch=getc();}
    return x;
}

void insert(int x,int y,int v)
{
    e[++len].nt=lin[x]; lin[x]=len; e[len].y=y; e[len].v=v; rev[len]=len+;
    e[++len].nt=lin[y]; lin[y]=len; e[len].y=x; e[len].v=; rev[len]=len-;
}

void init()
{
    n=read();m=read();
    s=;
    t=n;
    for(int i=;i<n;++i)     insert(i,i+n,);
    for(int i=;i<=m;++i)
    {
        int x=read(),y=read();
        if(x>y) std::swap(x,y);
        if(x!=)
        {
            insert(x+n,y,);
            insert(y+n,x,);
        }
        else
        {
            insert(,y,);
            insert(y,,);
        }
    }
}

bool make_level()
{
    int head=,tail=;
    q[]=s;
    memset(level,-,sizeof(level));
    level[s]=;
    while(head++<tail)
    {
        int x=q[head];
        for(int i=lin[x];i;i=e[i].nt)
            if(e[i].v && level[e[i].y]==-)
            {
                level[e[i].y]=level[x]+;
                q[++tail]=e[i].y;
            }
    }
    return level[t]>=;
}

int max_flow(int k,int flow)
{
    if(k==t) return flow;
    int maxflow=;
    int v;
    for(int i=lin[k];i && (maxflow<flow);i=e[i].nt)
        if(e[i].v && level[e[i].y]==level[k]+)
            if(v=max_flow(e[i].y,min(e[i].v,flow-maxflow)))
                maxflow+=v,e[i].v-=v,e[rev[i]].v+=v;
    if(!maxflow) level[k]=-;
    return maxflow;
}

void dinic()
{
    int v;
    while(make_level())
        while(v=max_flow(s,INF))
            ans+=v;
}

int main()
{
//    freopen("a.txt","r",stdin);
    init();
    dinic();
    using std::max;
    if(ans==) ans=;
    printf("%d\n",ans-);
    return ;
}