LightOJ - 1336 Sigma Function(约数和+整数拆分)

题干中给出函数公式：

　　

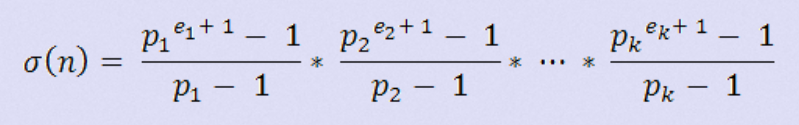
其中pi为n的每个素因数，ei为其个数。设该函数为F(x)，其意义为x的约数之和。问在1-n中有多少x,令F(x)为偶数。

分析：设f(p)为(p^(e+1)-1)/(p-1)。若F(x)为奇数，则任意的f(pi)都为奇数。

f(p)还可以写成：f(p)= (1+p^1+p^2+...+p^e)。则当p==2时，f(p)肯定是奇数（偶数+1）;当p!=2时，因为p是素数，所以p一定是奇数。则e偶数时，f(p)为奇数。

所以一个数x若可以表示为 (2^2k1)*(3^2k2)*(5^2k3)*....*(pn^2kn)的形式，即x是平方数或2x是平方数的时候，其F(x)为奇。

那么对给定的n，sqrt(n)+sqrt(n/2)的值就是1-n中约数和为奇数的个数。相减得到答案

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = ;

int main()
{
    #ifndef ONLINE_JUDGE
        freopen("in.txt","r",stdin);
        freopen("out.txt","w",stdout);
    #endif
    int T,N,a,cas=;
    LL n;
    scanf("%d",&T);
    while(T--){
        scanf("%lld",&n);
        LL ans = n - (LL)sqrt(n/) - (LL)sqrt(n);
        printf("Case %d: %lld\n",cas++,ans);
    }
    return ;
}