loadrunner11操作手册

一：操作

或者

增加用户数的方法

一：仅对单个场景增加用户数

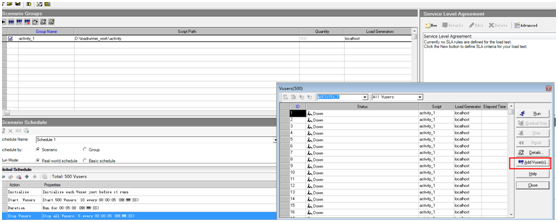
二：同时对多个场景增加用户数

第一步：

第二步：

二：脚本编写示例

Action()

{

int nHttpRetCode;

web_reg_save_param("ResponseBody", "LB=", "RB=", "Search=Body", LAST);

web_save_header(RESPONSE,"ResponseHeader");

lr_start_transaction("activity");

web_custom_request("get_test",

"URL=http://192.168.1.249:8088/mobile2/activity/list.json?resultType=0&userType=3",

"Method=GET",

"Resource=0",

"Referer=",

"Mode=HTTP",

"EncType=text/html;charset=UTF-8",

"Body=",

LAST);

lr_end_transaction("activity", LR_PASS);

//打印返回信息

lr_output_message("# 响应头信息：\n %s", lr_eval_string("{ResponseHeader}"));

//lr_output_message("# 响应原始内容体：\n %s", lr_eval_string("{ResponseBody}"));

lr_convert_string_encoding(lr_eval_string("{ResponseBody}"),LR_ENC_UTF8 ,LR_ENC_SYSTEM_LOCALE,"ResponseBodyUTF8");

lr_output_message("# 响应解码后内容体：\n %s", lr_eval_string("{ResponseBodyUTF8}"));

//获取服务器http响应码

nHttpRetCode = web_get_int_property(HTTP_INFO_RETURN_CODE);

if(nHttpRetCode == 200)

{  lr_output_message("Success!");   }

else

{  lr_output_message("Failed! ");    }

return 0;

}

三：测试报告查看

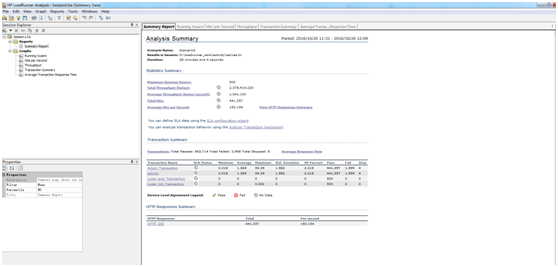
关注：

Transaction: Transaction Name 事务名称

Minimum 最小值

Average 平均值

Maximum 最大值

Std. Deviation 标准方差值

90 Percent 90% 响应时间

报告讲解：

1、90 Percent响应时间：表示该组中90%的用户都能在该时间内响应（完成该操作） 90 Percent 表示90%的用户在 0.xxx 秒内完成操作 可以通过Properties中 Percentile 90 可以修改 -> Additional Settings -> Transaction Percentile 若改为80，表示80%的用户。 再改回90%

2、一个事务，100用户执行，其中一个用户执行时间1000秒，其他99%的用户响应时间为0.001秒。 则该情况下90% 和 平均响应时间 哪个更准确？ 90 Percent

3、标准方差值：越小越好。越趋近于0，表示所有用户执行该事务的响应时间越接近，表示系统越稳定。

（数学中知识）

Mininum Average Maximum Std.Deviation

0.203    0.313   0.404   0.095

说明前面几个值比较接近，比较稳定。

4、网络带宽充足的情况下，当吞吐量（Throughput）随着点击率（Hits per second）的升高而升高，说明AUT的服务器处理能力充足。

四：测试报告导出

进行使用Analysis进行打开一份压力测试的报告，进入到界面中进行点击菜单中的Reports选项菜单。

 

 

1. 2

就会弹出了下拉菜单中进行选择为”new report“选项。

1. 3

然后就会在new report中进行填写为general、format、content进行在其中内容根据的需要进行填写，然后进行点击generate。

1. 4

然后就会弹出了一个word的文档的格式选项。进行对当前的word文档进行保存到本地的位置中，进行点击菜单中的“save”的选项。

1. 5

弹出了一个下拉的菜单中进行选择为“Microsoft word 2007 file”的选项。

1. 6

然后就会弹出了export settings的选项框，可以直接点击OK。

1. 7

进行选择为本地电脑的报告位置。

1. 8

word可以在本地电脑中找到该文件的报告，说明的是文件导出成功的。

生成html形式报告

五：测试结果分析

1. LoadRunner测试结果分析的第一步应该是查看分析综述（Analysis Summary），其包括统计综述（Statistics Summary）、事务综述（Transaction Summary）、HTTP 响应综述（HTTP Responses Summary）三部分。在统计综述中查看Total Errors的数量，HTTP 响应综述中查看HTTP 404数量，若数值相对较大（HTTP 404则相对于HTTP 200），则说明系统测试中出错较多，系统系能有问题；另外查看事务的平均响应时间和其90%的事务平均响应时间，若时间过长，超过测试计划中的要求值，则说明系统的性能不满足我们的要求。

2. 第二步对LoadRunner测试结果图进行分析，首先对事务综述（Transaction Summary）进行分析，该图可以直观地看出在测试时间内事务的成功与失败情况，所以比第一步更容易判断出被测系统运行是否正常。

3. 接着分析事务平均响应时间（Average Transaciton Response Time），若事务平均响应时间曲线趋高，则说明被测系统处理事务的速度开始逐渐变慢，即被测系统随着运行时间的变化，整体性能不断下降。当系统性能存在问题时，该曲线的走向一般表现为开始缓慢上升，然后趋于平稳，最后缓慢下降。原因是：被测系统处理事务能力下降，事务平均响应时间变长，在曲线上表现为缓慢上升；而并发事务达到一定数量时，被测系统无法处理多余的事务，此时曲线变现为趋于平稳；当一段时间后，事务不断被处理，其数量减少，在曲线上表现为下降。如果被测系统没有等待机制，那么事务响应时间会越来越长，最后系统崩溃。

4. 再分析每秒通过事务数（Transactions per Second/TPS），该曲线表示被测系统在运行的任意时刻，每个事务通过、失败的情况，其是考查系统性能的一个重要参数。若随着压力的增加，曲线如果开始变化缓慢或有平稳的趋势，则有可能是服务器开始出现瓶颈。

[5]. 分析每秒通过事务总数（Total Transactions per Second），该曲线显示在任意时刻被测系统通过的事务总数、失败的事务总数。该曲线走向和TPS曲线走向一致。

[6]. 事务性能摘要（Transaction Performance Sunmmary）该曲线表示被测系统中所有事务的最小、最大和平均事务响应时间。

[7]. 事务在负载情况下的响应时间（Transaction Response Time Under Load），该曲线表示在不同数量的虚拟用户情况下的事务响应时间情况。该图对分析具有渐变负载的测试场景比较有用。

[8]. 事务响应时间（百分比）（Transaction Response Time（Percentile）），该曲线可以容易地分析出在给定的响应时间范围内事务量的百分比重。

[9]. 事务响应时间（分布）（Transaction Response Time(Distribution)），该图可以容易地分析出在给定响应时间范围内的事务量情况。

其实，若并不是十分详细地分析测试结果，第4步与第5步选其一分析，第6步、第7步、第8步为可选项，因为在第1步就在一定程度上分析了，而第9步又与第8步功能相识。LoadRunner生成测试结果图在很大的程度上具有一定的重复性，只不过是在不同情况下的具体显示。

六：优化调整

（1）Tomcat  conf文件夹下的server.xml

<Connector port="8080" protocol="HTTP/1.1"

connectionTimeout="20000"

URIEncoding="UTF-8"

enableLookups="false"

disableUploadTimeout="true"

acceptCount="500"

maxThreads="500"

seURIValidationHack="false"

redirectPort="8443" />

（2）tomcat bin目录catalina.sh增加

JAVA_OPTS='-server -Xms1024m -Xmx1024m'