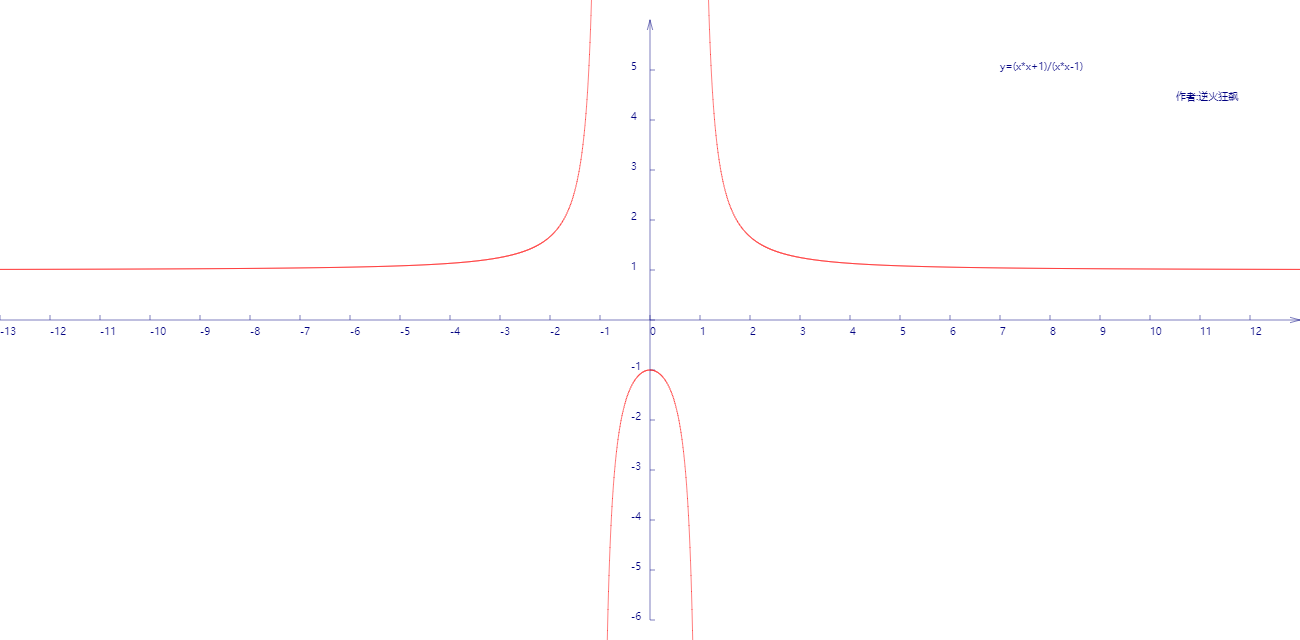
代码：

<!DOCTYPE html>
<html lang="utf-8">
<meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>
<head>
     <title>描绘函数(x*x+1)/(x*x-1)曲线</title>
    </head>

     <body onload="draw()">
        <canvas id="myCanvus" width="1300px" height="640px" style="border:1px dashed black;">
            出现文字表示你的浏览器不支持HTML5
        </canvas>
     </body>
</html>
<script type="text/javascript">
<!--
    function draw(){
        var canvas=document.getElementById("myCanvus");
        var canvasWidth=1300;
        var canvasHeight=640;

        var context=canvas.getContext("2d");

        context.fillStyle = "white";
        context.fillRect(0, 0, canvasWidth, canvasHeight);

        context.strokeStyle = "black";
        context.fillStyle = "black";

        // 进行坐标变换：把原点放在左下角，东方为X轴正向，北方为Y轴正向
        var offsetY=320;// Y向偏移值，正值向上偏，用来画坐标轴
        var offsetX=650;// X向偏移值，正值向右偏，用来画坐标轴

        context.save();
        context.translate(0+offsetX,canvasHeight-offsetY);

        drawAxisXText(context);// 文字和线分开画比较好处理
        drawAxisYText(context);
        drawTitleText(context);

        context.rotate(getRad(180));
        context.scale(-1,1);        

        drawAxisX(context);
        drawAxisY(context);
        drawCurve(context);       

        context.restore();
    }

    function drawTitleText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var x=350;
        var y=-250;

        // 写文字
        ctx.fillText("y=(x*x+1)/(x*x-1)",x,y);        

        ctx.fillText("  作者:逆火狂飙",x+170,y+30);
    }

    function drawCurve(ctx){
        var SU=50;// Scale Unit

        var cds=[{}];
        var cds1=[{}];
        var cds2=[{}];

        var x,y;
        for(x=-13;x<=13;x+=0.01){
            if(x<-1-0.01){// 0.01 防止除零溢出
                y=(x*x+1)/(x*x-1);// 函数式在此
                var arr={"x":x,"y":y};
                cds.push(arr);
            }

            if(x>1){
                y=(x*x+1)/(x*x-1);// 函数式在此
                var arr={"x":x,"y":y};
                cds1.push(arr);
            }

            if(x>-1 && x<1){
                y=(x*x+1)/(x*x-1);// 函数式在此
                var arr={"x":x,"y":y};
                cds2.push(arr);
            }
        }

        ctx.strokeStyle = "red";

        ctx.beginPath();
        console.log("cds.length="+cds.length);
        for(var i=0; i<cds.length; i++){
            console.log("12="+cds[i]);
            ctx.lineTo(cds[i].x*SU,cds[i].y*SU);
        } 

        ctx.stroke();
        ctx.closePath();

        ctx.beginPath();
        for(var i=0; i<cds1.length; i++){
            ctx.lineTo(cds1[i].x*SU,cds1[i].y*SU);
        } 

        ctx.stroke();
        ctx.closePath();

        ctx.beginPath();
        for(var i=0; i<cds2.length; i++){
            ctx.lineTo(cds2[i].x*SU,cds2[i].y*SU);
        } 

        ctx.stroke();
        ctx.closePath();
    }

    function drawAxisX(ctx){
        ctx.save();

        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(start, 0);
        ctx.lineTo(end, 0);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(end-Math.cos(getRad(15))*10, Math.sin(getRad(15))*10);
        ctx.lineTo(end, 0);
        ctx.lineTo(end-Math.cos(getRad(15))*10, -Math.sin(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();

        // 画刻度
        var x,y;
        y=5;
        for(x=start;x<end;x+=50){
            ctx.beginPath();
            ctx.moveTo(x, 0);
            ctx.lineTo(x, y);

            ctx.stroke();
            ctx.closePath();
        }

        ctx.restore();
    }

    function drawAxisXText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-650;
        var end=650;

        // 写文字
        var x,y=5;
        for(x=start;x<end;x+=50){
            ctx.fillText(x/50,x,y+10);
        }
    }

    function drawAxisY(ctx){
        ctx.save();

        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-300;
        var end=300;

        // 画轴
        ctx.beginPath();
        ctx.moveTo(0, start);
        ctx.lineTo(0, end);
        ctx.stroke();
        ctx.closePath();

        // 画箭头
        ctx.beginPath();
        ctx.moveTo(Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.lineTo(0, end);
        ctx.lineTo(-Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
        ctx.stroke();
        ctx.closePath();

        // 画刻度
        var x,y;
        x=5;
        for(y=start;y<end;y+=50){
            ctx.beginPath();
            ctx.moveTo(x, y);
            ctx.lineTo(0, y);

            ctx.stroke();
            ctx.closePath();
        }
    }

    function drawAxisYText(ctx){
        ctx.lineWidth=0.5;
        ctx.strokeStyle='navy';
        ctx.fillStyle='navy';

        var start=-250;
        var end=350;

        // 写文字
        var x=-19,y=5;
        for(y=start;y<end;y+=50){

            if(y!=0){
                ctx.fillText(-y/50,x,y);
            }
        }
    }

    function getRad(degree){
        return degree/180*Math.PI;
    }

    function cutShort(str,length){
        if(str.length>length){
            str=str.substr(0,length)+"...";
        }

        return str;
    }
//-->
</script>

在笛卡尔坐标系上描绘函数(x*x+1)/(x*x-1)曲线的更多相关文章

  1. 在笛卡尔坐标系上描绘函数2*x+Math.sqrt(5-x*x)及其共轭函数2*x-Math.sqrt(5-x*x)曲线

    代码如下: <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Ty ...

  2. 在笛卡尔坐标系上描绘函数 y=4x^2-2/4x-3

    代码: <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type ...

  3. 在笛卡尔坐标系上描绘y=x^2-4/x^2-2x-3曲线

    <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type&quo ...

  4. AcWing：112. 雷达设备（贪心 + 笛卡尔坐标系化区间）

    假设海岸是一条无限长的直线,陆地位于海岸的一侧,海洋位于另外一侧. 每个小岛都位于海洋一侧的某个点上. 雷达装置均位于海岸线上,且雷达的监测范围为d,当小岛与某雷达的距离不超过d时,该小岛可以被雷达覆 ...

  5. 如果是在有master上开启了该参数，记得在slave端也要开启这个参数（salve需要stop后再重新start），否则在master上创建函数会导致replaction中断。

    如果是在有master上开启了该参数,记得在slave端也要开启这个参数(salve需要stop后再重新start),否则在master上创建函数会导致replaction中断.

  6. 自学Linux Shell16.4-在命令行上使用函数

    点击返回 自学Linux命令行与Shell脚本之路 16.4-在命令行上使用函数 脚本函数不仅可以用作shell脚本命令,也可以用作命令行界面的命令.一旦在shell中定义了函数,可以从系统的任意目录 ...

  7. HTML5 Canvas 笛卡尔坐标系转换尝试

    <!DOCTYPE html> <html lang="utf-8"> <meta http-equiv="Content-Type&quo ...

  8. Javascript作业—数组去重（要求：原型链上添加函数）

    数组去重(要求:原型链上添加函数) <script> //数组去重,要求:在原型链上添加函数 //存储不重复的--仅循环一次 if(!Array.prototype.unique1){ A ...

  9. js进阶 12-8 如何知道上一个函数的返回值是什么（如何判断上一个函数是否执行成功）

    js进阶 12-8 如何知道上一个函数的返回值是什么(如何判断上一个函数是否执行成功) 一.总结 一句话总结:event的result属性即可. 1.event的result属性的实际应用场景是什么? ...

随机推荐

  1. java线程基本知识

    如何去定义一个线程?(三种方式)    1.Thread:继承这个类,然后重写run方法:将业务逻辑或任务写到run方法中,然后调用start来启动线程:    2.Runnable: 实现这个接口, ...

  2. No module named '_Sqlite3' 解决方法

    今晚,在学习Python的时候,(学习链接:http://yidao620c.github.io/blog/20150420/simpleblog-01.html(搭载自己的博客案例)): 想为系统生 ...

  3. HDU 6118 2017百度之星初赛B 度度熊的交易计划（费用流）

    度度熊的交易计划 Time Limit: 12000/6000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)Total S ...

  4. mysql中timestamp类型的应用

    在开发过程中我们一般需要记住某条记录的创建时间,在MySQL中如果使用dateTime类型的话,无法设定默认值,我们可以采用timestamp类型来记录创建时间.但是随之而来的有个问题,比如说你的这个 ...

  5. POJ - 1835 宇航员（模拟题）

    问题描述: 宇航员在太空中迷失了方向,在他的起始位置现在建立一个虚拟xyz坐标系,称为绝对坐标系,宇航员正面的方向为x轴正方向,头顶方向为z轴正方向,则宇航员的初始状态如下图所示: 现对六个方向分别标 ...

  6. 【BZOJ 2212】【POI 2011】Tree Rotations

    http://www.lydsy.com/JudgeOnline/problem.php?id=2212 自下而上贪心. 需要用权值线段树来记录一个权值区间内的出现次数. 合并线段树时统计逆序对的信息 ...

  7. 【Tarjan】【LCA】【动态规划】【推导】hdu6065 RXD, tree and sequence

    划分出来的每个区间的答案,其实就是连续两个的lca的最小值. 即5 2 3 4 这个区间的答案是min(dep(lca(5,2)),dep(lca(2,3),dep(lca(3,4)))). 于是dp ...

  8. 【凸包】【三分】Gym - 101309D - Dome of Circus

    容易发现,圆锥体积和点的具体x.y坐标无关,只与其到z轴的距离sqrt(x*x+y*y)有关. 于是将这些三维的点都投射到二维的xOy平面的第二象限(sqrt(x*x+y*y),z),求个上凸壳,然后 ...

  9. 【Heap-dijkstra】CDOJ1639 云中谁寄锦书来？雁字回时，月满西楼。

    题意: 在n个点m条边的无向图上,有k个出口 从起点出发,每到一个点(包括起点),该点连出的边中有d条会被封锁 求最坏情况下到达出口的最短路 题解: 该题为dijkstra算法的拓展 由于求最坏情况下 ...

  10. 【容斥原理】【分解质因数】poj1091 跳蚤

    题意转化为求一个线性组合a1*x1+a2*x2+...+an*xn+m*xn+1=1在什么时候可以有解.(ai在1~m的范围内任取) 易得当且仅当gcd(a1,a2,...,an)=1时可能有解. 然 ...