【最小乘积生成树】bzoj2395[Balkan 2011]Timeismoney

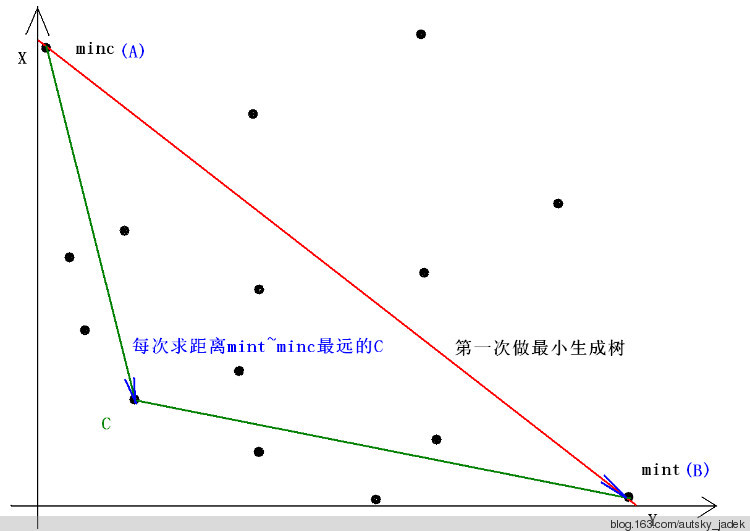
设每个点有x,y两个权值，求一棵生成树，使得sigma(x[i])*sigma(y[i])最小。

设每棵生成树为坐标系上的一个点，sigma(x[i])为横坐标，sigma(y[i])为纵坐标。则问题转化为求一个点，使得xy=k最小。即，使过这个点的反比例函数y=k/x最接近坐标轴。

Step1:求得分别距x轴和y轴最近的生成树（点）：A、B（分别按x权值和y权值做最小生成树即可）。

Step2:寻找一个在AB的靠近原点一侧的且离AB最远的生成树C，试图更新答案。

【怎么找？？？？

——由于C离AB最远，所以S△ABC面积最大。

向量AB=（B.x - A.x , B.y - A.y）

向量AC= (C.x - A.x , C.y - A.y)

向量AB、AC的叉积(的二分之一)为S△ABC的面积（只不过叉积是有向的，是负的，所以最小化这个值，即为最大化面积）。

最小化：(B.x-A.x)*(C.y-A.y)-(B.y-A.y)*(C.x-A.x)

=(B.x-A.x)*C.y+(A.y-B.y)*C.x  -  A.y*(B.x-A.x)+A.x*(B.y-A.y)/*粗体为常数，不要管*/

所以将每个点的权值修改为 y[i]*(B.x-A.x)+(A.y-B.y)*x[i] 做最小生成树，找到的即是C。】

Step3:递归地分别往AC、BC靠近原点的一侧找。递归边界：该侧没有点了(即叉积大于等于零)。

BZOJ2395 裸题

Code:

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 int res;
 char c;
 inline int Get()
 {
     res=;c='*';
     while(c<''||c>'')c=getchar();
     while(c>=''&&c<=''){res=res*+(c-'');c=getchar();}
     return res;
 }
 struct Edge{int u,v,c,t,w;void read(){u=Get();v=Get();c=Get();t=Get();}};
 struct Point{int x,y;Point(const int &A,const int &B){x=A;y=B;}Point(){}};
 typedef Point Vector;
 typedef long long LL;
 Vector operator - (const Point &a,const Point &b){return Vector(a.x-b.x,a.y-b.y);}
 int Cross(Vector A,Vector B){return A.x*B.y-A.y*B.x;}
 bool operator < (const Edge &a,const Edge &b){return a.w<b.w;}
 Edge edges[];
 int n,m,rank[],fa[];
 Point ans=Point(,),minc,mint;
 inline void init()
 {
     memset(rank,,sizeof(rank));
     for(int i=;i<n;i++)
       fa[i]=i;
 }
 int findroot(int x)
 {
     if(fa[x]==x)
       return x;
     int t=findroot(fa[x]);
     fa[x]=t;
     return t;
 }
 inline void Union(int U,int V)
 {
     if(rank[U]<rank[V])
       fa[U]=V;
     else
       {
         fa[V]=U;
         if(rank[U]==rank[V])
           rank[U]++;
       }
 }
 inline Point Kruscal()
 {
     int tot=;
     Point now=Point(,);
     init();
     for(int i=;i<=m;i++)
       {
           int U=findroot(edges[i].u),V=findroot(edges[i].v);
           if(U!=V)
             {
                 Union(U,V);
                 tot++;
                 now.x+=edges[i].c;
                 now.y+=edges[i].t;
                 if(tot==n-)
                   break;
             }
       }
     LL Ans=(LL)ans.x*ans.y,Now=(LL)now.x*now.y;
     if( Ans>Now || (Ans==Now&&now.x<ans.x) )
       ans=now;
     return now;
 }
 void Work(Point A,Point B)
 {
     for(int i=;i<=m;i++)
       edges[i].w=edges[i].t*(B.x-A.x)+edges[i].c*(A.y-B.y);
     sort(edges+,edges+m+);
     Point C=Kruscal();
     if(Cross(B-A,C-A)>=)
       return;
     Work(A,C);
     Work(C,B);
 }
 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;i++)
       edges[i].read();
     for(int i=;i<=m;i++)
       edges[i].w=edges[i].c;
     sort(edges+,edges+m+);
     minc=Kruscal();
     for(int i=;i<=m;i++)
       edges[i].w=edges[i].t;
     sort(edges+,edges+m+);
     mint=Kruscal();
     Work(minc,mint);
     printf("%d %d\n",ans.x,ans.y);
     return ;
 }