poj1691

Painting A Board

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3642		Accepted: 1808

Description

The CE digital company has built an Automatic Painting Machine (APM) to paint a flat board fully covered by adjacent non-overlapping rectangles of different sizes each with a predefined color. 

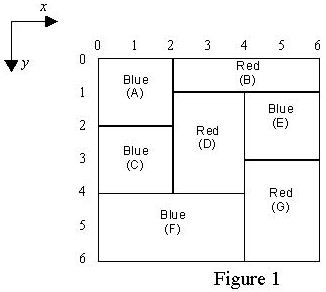
To color the board, the APM has access to a set of brushes. Each brush has a distinct color C. The APM picks one brush with color C and paints all possible rectangles having predefined color C with the following restrictions: 
To avoid leaking the paints and mixing colors, a rectangle can only be painted if all rectangles immediately above it have already been painted. For example rectangle labeled F in Figure 1 is painted only after rectangles C and D are painted. Note that each rectangle must be painted at once, i.e. partial painting of one rectangle is not allowed. 
You are to write a program for APM to paint a given board so that the number of brush pick-ups is minimum. Notice that if one brush is picked up more than once, all pick-ups are counted. 

Input

The first line of the input file contains an integer M which is the number of test cases to solve (1 <= M <= 10). For each test case, the first line contains an integer N, the number of rectangles, followed by N lines describing the rectangles. Each rectangle R is specified by 5 integers in one line: the y and x coordinates of the upper left corner of R, the y and x coordinates of the lower right corner of R, followed by the color-code of R. 
Note that: 

1. Color-code is an integer in the range of 1 .. 20.
2. Upper left corner of the board coordinates is always (0,0).
3. Coordinates are in the range of 0 .. 99.
4. N is in the range of 1..15.

Output

One line for each test case showing the minimum number of brush pick-ups.

Sample Input

1
7
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2

Sample Output

3

Source

Tehran 1999

大致题意：

墙上有一面黑板，现划分为多个矩形，每个矩形都要涂上一种预设颜色C。

由于涂色时，颜料会向下流，为了避免处于下方的矩形的颜色与上方流下来的颜料发生混合，要求在对矩形i着色时，处于矩形i上方直接相邻位置的全部矩形都必须已填涂颜色。

在填涂颜色a时，若预设颜色为a的矩形均已着色，或暂时不符合着色要求，则更换新刷子，填涂颜色b。

注意：

1、  当对矩形i涂色后，发现矩形i下方的矩形j的预设颜色与矩形i一致，且矩形j上方的全部矩形均已涂色，那么j符合填涂条件，可以用 填涂i的刷子对j填涂，而不必更换新刷子。

2、  若颜色a在之前填涂过，后来填涂了颜色b，现在要重新填涂颜色a，还是要启用新刷子，不能使用之前用于填涂颜色a的刷子。

3、  若颜色a在刚才填涂过，现在要继续填涂颜色a，则无需更换新刷子。

4、  矩形着色不能只着色一部分，当确认对矩形i着色后，矩形i的整个区域将被着色。

首先要注意输入数据，每个矩形信息的输入顺序是 y x y x c，而不是 x y x y c

若弄反了x y坐标怎样也不会AC的.....

解题思路:

1. 染色问题. 先将图建立起来. 将当前小矩阵编号为i, 与其相邻的或则在上面的矩阵链接起来.(做标记)

2. 深搜解决. dfs(int nowlen,int ans,int color)
nowlen: 小矩阵已经染色的数目, ans: 当前使用画刷的次数. color: 当前画刷的颜色.

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
#define inf 0x3f3f3f3f
#define N 20
struct node{
    int x1,y1,x2,y2,color;
}e[N];
int map[N][N],deg[N],vis[N];
int result,n;
void read_graph(){
    for(int i=;i<=n;i++)
        for(int j=;j<=n;j++)
            if(e[i].y2==e[j].y1&&(e[j].x1<=e[i].x2&&e[i].x1<=e[j].x2))
                deg[j]++,map[i][j]=;
}
void dfs(int nowlen,int ans,int color){
    if(ans>result) return ;
    if(nowlen==n){
        result=ans;return ;
    }
    for(int i=;i<=n;i++){
        if(!vis[i]&&!deg[i]){
            vis[i]=;
            for(int j=;j<=n;j++)
                if(map[i][j])
                    deg[j]--;
            if(e[i].color==color)
                dfs(nowlen+,ans,color);
            else
                dfs(nowlen+,ans+,e[i].color);
            vis[i]=;
            for(int j=;j<=n;j++)
                if(map[i][j])
                    deg[j]++;
        }
    }
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        memset(map,,sizeof map);
        memset(deg,,sizeof deg);
        memset(vis,,sizeof vis);
        scanf("%d",&n);
        for(int i=;i<=n;i++)
            scanf("%d%d%d%d%d",&e[i].y1,&e[i].x1,&e[i].y2,&e[i].x2,&e[i].color);
        result=inf;
        read_graph();
        dfs(,,);
        printf("%d\n",result);
    }
    return ;
}