【BZOJ4259】残缺的字符串 FFT

【BZOJ4259】残缺的字符串

Description

很久很久以前，在你刚刚学习字符串匹配的时候，有两个仅包含小写字母的字符串A和B，其中A串长度为m，B串长度为n。可当你现在再次碰到这两个串时，这两个串已经老化了，每个串都有不同程度的残缺。

你想对这两个串重新进行匹配，其中A为模板串，那么现在问题来了，请回答，对于B的每一个位置i，从这个位置开始连续m个字符形成的子串是否可能与A串完全匹配?

Input

第一行包含两个正整数m,n(1<=m<=n<=300000)，分别表示A串和B串的长度。

第二行为一个长度为m的字符串A。

第三行为一个长度为n的字符串B。

两个串均仅由小写字母和*号组成，其中*号表示相应位置已经残缺。

Output

第一行包含一个整数k，表示B串中可以完全匹配A串的位置个数。

若k>0，则第二行输出k个正整数，从小到大依次输出每个可以匹配的开头位置（下标从1开始）。

Sample Input

3 7
a*b
aebr*ob

Sample Output

2
1 5

题解：我们令?代表的T值=0，然后设出这样一个式子

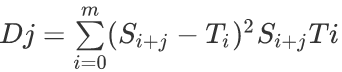
这样一来，只要T和S在j位置匹配，当且仅当Dj=0，然后我们将这个式子拆开，变成下面那样

然后将T反转，就变成了卷积的形式，分别将它们6个求出来计算就好了

#include <cstdio>
#include <cstring>
#include <iostream>
#include <cmath>
#define pi acos(-1.0)
using namespace std;
struct cp
{
	double x,y;
	cp (double a,double b){x=a,y=b;}
	cp (){}
	cp operator + (cp a){return cp(x+a.x,y+a.y);}
	cp operator - (cp a){return cp(x-a.x,y-a.y);}
	cp operator * (cp a){return cp(x*a.x-y*a.y,x*a.y+y*a.x);}
}n1[1<<20],n2[1<<20],n3[1<<20],n4[1<<20],n5[1<<20],n6[1<<20];
int n,m,top;
char s1[1<<20],s2[1<<20];
int s[1<<20],t[1<<20],sta[1<<20];
void FFT(cp *a,int len,int f)
{
	int i,j,k,h;
	cp t;
	for(i=k=0;i<len;i++)
	{
		if(i>k)	swap(a[i],a[k]);
		for(j=(len>>1);(k^=j)<j;j>>=1);
	}
	for(h=2;h<=len;h<<=1)
	{
		cp wn(cos(f*2*pi/h),sin(f*2*pi/h));
		for(j=0;j<len;j+=h)
		{
			cp w(1,0);
			for(k=j;k<j+h/2;k++)	t=w*a[k+h/2],a[k+h/2]=a[k]-t,a[k]=a[k]+t,w=w*wn;
		}
	}
}
int main()
{
	scanf("%d%d%s%s",&m,&n,s2,s1);
	int i,len=1;
	while(len<n+m)	len<<=1;
	for(i=0;i<n;i++)	s[i]=(s1[i]=='*')?0:(s1[i]-'a'+1);
	for(i=0;i<m;i++)	t[m-i-1]=(s2[i]=='*')?0:(s2[i]-'a'+1);
	for(i=0;i<n;i++)	n1[i]=cp(s[i]*s[i]*s[i],0),n2[i]=cp(-2*s[i]*s[i],0),n3[i]=cp(s[i],0);
	for(i=0;i<m;i++)	n4[i]=cp(t[i],0),n5[i]=cp(t[i]*t[i],0),n6[i]=cp(t[i]*t[i]*t[i],0);
	FFT(n1,len,1),FFT(n2,len,1),FFT(n3,len,1),FFT(n4,len,1),FFT(n5,len,1),FFT(n6,len,1);
	for(i=0;i<len;i++)	n1[i]=n1[i]*n4[i]+n2[i]*n5[i]+n3[i]*n6[i];
	FFT(n1,len,-1);
	for(i=0;i<n-m+1;i++)	if(!(int)(n1[i+m-1].x/len+0.1))	sta[++top]=i+1;
	printf("%d\n",top);
	for(i=1;i<top;i++)	printf("%d ",sta[i]);
	if(top)	printf("%d",sta[top]);
	return 0;
}