一道算法题-八皇后问题(C++实现)

八皇后问题

一、题意解析

　　国际象棋中的皇后，可以横向、纵向、斜向移动。如何在一个8X8的棋盘上放置8个皇后，使得任意两个皇后都不在同一条横线、竖线、斜线方向上？八皇后问题是一个古老的问题，于1848年由一位国际象棋棋手提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，如何求解？以高斯为代表的许多数学家先后研究过这个问题。后来，当计算机问世，通过计算机程序的运算可以轻松解出这个问题。

二、如何解决八皇后问题？

　　所谓递归回溯，本质上是一种枚举法。这种方法从棋盘的第一行开始尝试摆放第一个皇后，摆放成功后，递归一层，再遵循规则在棋盘第二行来摆放第二个皇后。如果当前位置无法摆放，则向右移动一格再次尝试，如果摆放成功，则继续递归一层，摆放第三个皇后......

　　如果某一层看遍了所有格子，都无法成功摆放，则回溯到上一个皇后，让上一个皇后右移一格，再进行递归。如果八个皇后都摆放完毕且符合规则，那么就得到了其中一种正确的解法。说起来有些抽象，我们来看一看递归回溯的详细过程。

　　1.第一层递归，尝试在第一行摆放第一个皇后：

　　2.第二层递归，尝试在第二行摆放第二个皇后（前两格被第一个皇后封锁，只能落在第三格）：

　　3.第三层递归，尝试在第三行摆放第三个皇后（前四格被第一第二个皇后封锁，只能落在第五格）：

　　4.第四层递归，尝试在第四行摆放第四个皇后（第一格被第二个皇后封锁，只能落在第二格）：

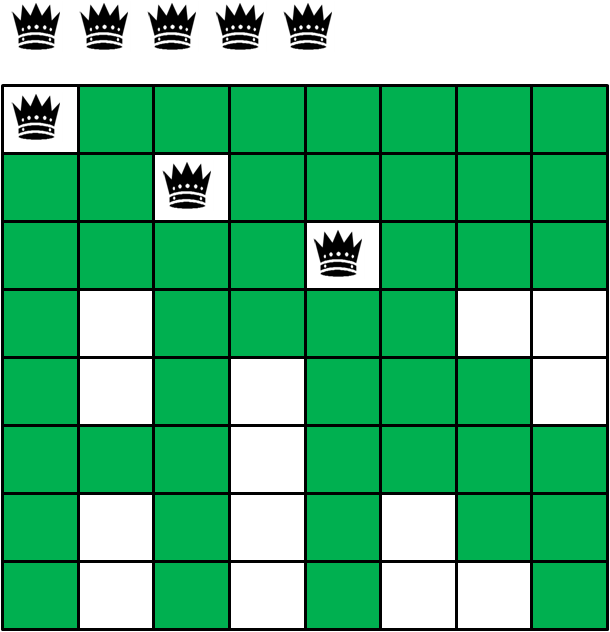
　　5.第五层递归，尝试在第五行摆放第五个皇后（前三格被前面的皇后封锁，只能落在第四格）：

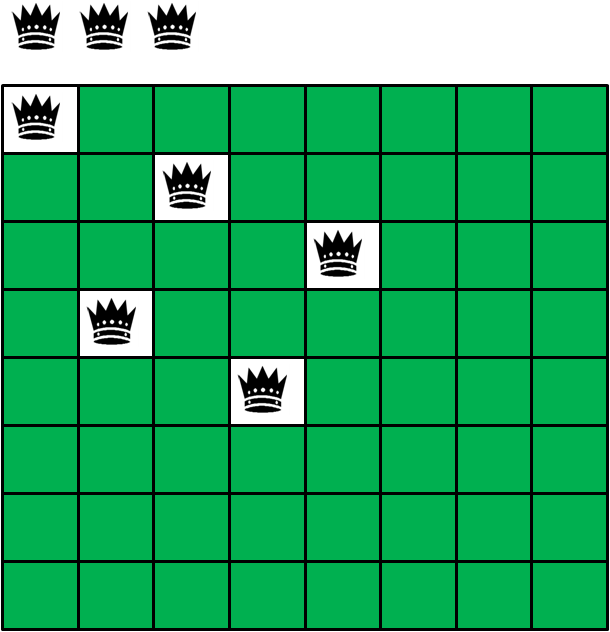
　　6.由于所有格子都“绿了”，第六行已经没办法摆放皇后，于是进行回溯，重新摆放第五个皇后到第八格。：

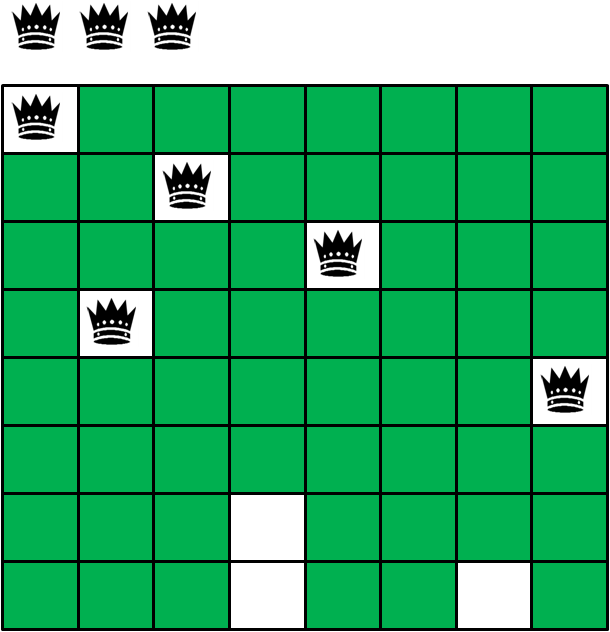
　　7.第六行仍然没有办法摆放皇后，第五行也已经尝试遍了，于是回溯到第四行，重新摆放第四个皇后到第七格。：

　　8.继续摆放第五个皇后，以此类推......

三、八皇后问题的代码实现

　　解决八皇后问题，可以分为两个层面：

1.找出第一种正确摆放方式，也就是深度优先遍历。

2.找出全部的正确摆放方式，也就是广度优先遍历。

我们本篇只介绍如何找出第一种正确摆放方式。具体代码如下：

 //"八皇后问题回溯实现"
 #include <iostream>
 using namespace std;
 const int ArSize = ;//这个数等于几，就是几皇后。
 int num = ;
 void solve(bool arr[ArSize][ArSize], int row);
 bool check(bool arr[ArSize][ArSize], int row, int column);
 void outPut(bool arr[ArSize][ArSize]);

 int main()
 {
     bool chessboard[ArSize][ArSize];
     // 数组初始化
     for (auto &i : chessboard)
     {
         for (auto &j : i)
         {
             j = false;
         }
     }
     solve(chessboard, );
     cout << "八皇后问题共有" << num << "种解！" << endl;
     system("pause");
     return ;
 }
 // 回溯法
 void solve(bool arr[ArSize][ArSize], int row)
 {
     for (int column = ; column < ArSize; ++column)
     {
         arr[row][column] = true;
         if (check(arr, row, column))
         {
             if (row +  == ArSize)
             {
                 outPut(arr);
             }
             else
             {
                 solve(arr, row + );
             }
         }
         arr[row][column] = false;
     }
 }
 // 判断皇后的落点是否合规
 bool check(bool arr[ArSize][ArSize], int row, int column)
 {
     if (row == )
     {
         return true;
     }
     int i, j;
     // 判断纵向是否有冲突
     for (i = ; i < row; ++i)
     {
         if (arr[i][column])
         {
             return false;
         }
     }
     i = row - ;
     j = column - ;
     // 判断正斜对角线是否有冲突
     while (i >=  && j >= )
     {
         if (arr[i][j])
         {
             return false;
         }
         --i;
         --j;
     }
     i = row - ;
     j = column + ;
     // 判断负斜对角线是否有冲突
     while (i >=  && j <= ArSize - )
     {
         if (arr[i][j])
         {
             return false;
         }
         --i;
         ++j;
     }
     return true;
 }
 // 打印每种正确的解法
 void outPut(bool arr[ArSize][ArSize])
 {
     ++num;
     cout << "**********************" << num << "*********************" << endl;
     for (int i = ; i < ArSize; ++i)
     {
         for (int j = ; j < ArSize; ++j)
         {
             cout << arr[i][j] << " ";
         }
         cout << endl;
     }
     cout << "*********************************************" << endl;
 }

　　输出结果的部分截图如下：

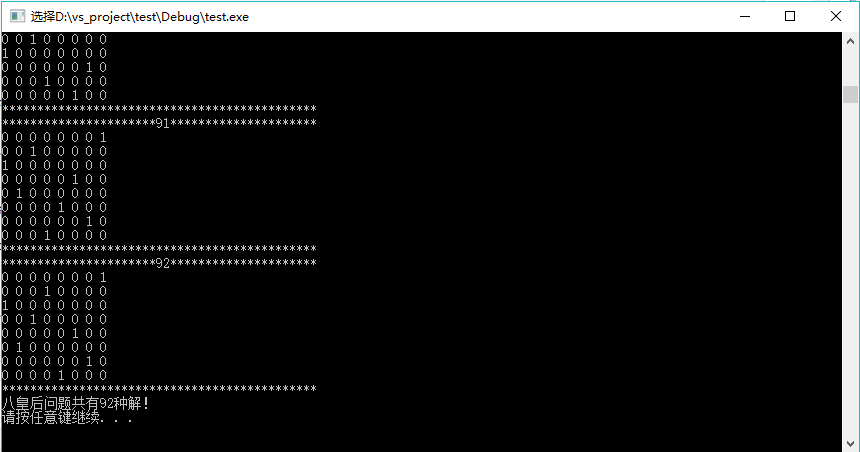
参考资料：

http://www.cnblogs.com/yonggandefeng/p/6275861.html