bzoj 3202 [Sdoi2013]项链——容斥+置换+推式子

题目：https://www.lydsy.com/JudgeOnline/problem.php?id=3202

可见Zinn博客：https://www.cnblogs.com/Zinn/p/10073897.html

关于算有序三元组那个部分，自己觉得是这样解释：

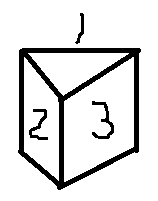这样标号的话，旋转置换有2个：(1,2,3)和(1,3,2)； 不动的话是一个置换：(1)(2)(3)； 翻转的话，贴着一个侧面所在的面上下翻转，就是三个置换：(1)(2,3)、(2)(1,3)、(3)(1,2)。根据Polya定理算不动点个数，就是 \( \frac{1}{6}(2*g(1)+g(3)+3*g(2) \) ，其中 g(x) 表示选 x 个数且其gcd=1的方案数。（比如 (1,2,3) ，如果“不动”的话，3个位置的数都要一样，即找1个数，是g(1)；(1)(2,3)的话，2、3位置的数一样，即找两个数，是g(2)）。

通过 dfs 质因数的幂来找出所有约数的方法很好，因为可以顺便做出 phi 。

注释掉的那个快速乘好像会 WA ？

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int N=1e7+,mod=1e9+,base=1e5;
ll M=(ll)(1e9+)*(ll)(1e9+);//(ll)!!!!!
int a,T,pri[N],cnt;ll n,t,u[N],ans,p[],q[],tot,tmd;
bool vis[N],fx;
void upd(ll &x,ll md){x>=md?x-=md:;x<?x+=md:;}
/*ll mul(ll a,ll b,ll md)
{ll ret=0;while(b){if(b&1ll)ret+=a,upd(ret,md);a+=a;upd(a,md);b>>=1ll;}return ret;}*/
/*ll mul(ll a,ll b,ll md)//slow and WA?
{
  ll bs=(md==M?mod:base);
  ll A=a/bs,B=a%bs,C=b/bs,D=b%bs;
  ll ret=A*C%md*bs%md*bs%md;
  ret=(ret+A*D%md*bs)%md;
  ret=(ret+B*C%md*bs)%md;
  ret=(ret+B*D)%md;
  return ret;
  }
*/
ll mul(ll a,ll b,ll md)
{
  return (a*b-(ll)( ((long double)a*b+0.5)/(long double)md )*md+md)%md;
}
ll pw(ll x,ll k,ll md)
{x%=md;k%=(md-);ll ret=;while(k){if(k&)ret=mul(ret,x,md);x=mul(x,x,md);k>>=;}return ret;}
void calc(ll md)
{
  ll g2=,g3=;
  for(int i=,j,d;i<=a;i=j+)
    {
      d=a/i; j=a/d; ll k=u[j]-u[i-];upd(k,md);
      ll tmp=mul(mul(d,d,md),k,md);
      g2=g2+tmp; upd(g2,md);
      tmp=mul(tmp,d,md);
      g3=g3+tmp; upd(g3,md);
    }
  t=(g3+*g2+)%md;
  t=mul(t,pw(,fx?M-mod-:mod-,md),md);//phi(M)=mod*(mod-1)
}
void init()
{
  memset(vis,,sizeof vis); cnt=;
  u[]=;  ll d;
  for(int i=;i<=a;i++)
    {
      if(!vis[i])u[i]=-,pri[++cnt]=i;
      for(int j=;j<=cnt&&(d=(ll)i*pri[j])<=a;j++)
    {
      vis[d]=;u[d]=-u[i];
      if(i%pri[j]==){u[d]=;break;}
    }
    }
  for(int i=;i<=a;i++)u[i]+=u[i-],upd(u[i],tmd);
  calc(tmd);
}
ll F(ll x,ll md)
{
  ll ret=;
  if(x&1ll)ret=-t; else ret=t-;
  upd(ret,md);
  ret+=pw(t-,x,md); upd(ret,md);
  return ret;
}
ll Phi(ll x,ll md)
{
  ll ret=x,yx=x;
  for(ll d=;d*d<=x;d++)
    if(x%d==)
      {
    ret/=d; ret*=(d-);
    while(x%d==)x/=d;
      }
  if(x>)ret/=x,ret*=(x-);
  return ret%md;
}
void cal(ll x)
{
  tot=;
  for(ll i=;i*i<=x;i++)
    if(x%i==)
      {
    p[++tot]=i;q[tot]=;
    while(x%i==)x/=i,q[tot]++;
      }
  if(x>)p[++tot]=x,q[tot]=;
}
void dfs(int cr,ll nw,ll phi)
{
  if(cr>tot){ans+=mul(F(n/nw,tmd),phi,tmd);upd(ans,tmd);return;}
  dfs(cr+,nw,phi);
  nw*=p[cr];phi*=p[cr]-;//needn't tmd
  dfs(cr+,nw,phi);
  for(int i=;i<=q[cr];i++)
    nw*=p[cr],phi*=p[cr],dfs(cr+,nw,phi);
}
int main()
{
  scanf("%d",&T);
  while(T--)
    {
      scanf("%lld%d",&n,&a);
      fx=(n%mod==); if(fx)tmd=M; else tmd=mod;
      init();  ans=;
      cal(n); dfs(,,);
      /*
      for(ll d=1;d*d<=n;d++)//d=1
    if(n%d==0)
      {
        ll k=n/d;
        ans+=mul(F(d,md),Phi(k,md),md); upd(ans,md);
        if(k!=d)ans+=mul(F(k,md),Phi(d,md),md), upd(ans,md);//mul
      }
      */
      if(fx)ans/=mod,ans=ans*pw(n/mod,mod-,mod)%mod;
      else ans=ans*pw(n,mod-,mod)%mod;
      printf("%lld\n",ans);
    }
  return ;
}