后缀自动机SAM学习笔记

前言(2019.1.6)

已经是二周目了呢...

之前还是有一些东西没有理解到位

重新写一下吧

后缀自动机的一些基本概念

参考资料和例子 from hihocoder

DZYO神仙翻译的神仙论文

简而言之，后缀自动机(SAM),是一个有限状态自动机(DFA)

SAM分为两个部分，一部分是一个Dag，另一部分是Parent树。——laofu

搬一个图下来(这是字符串\(aabbabd\)的\(SAM\))

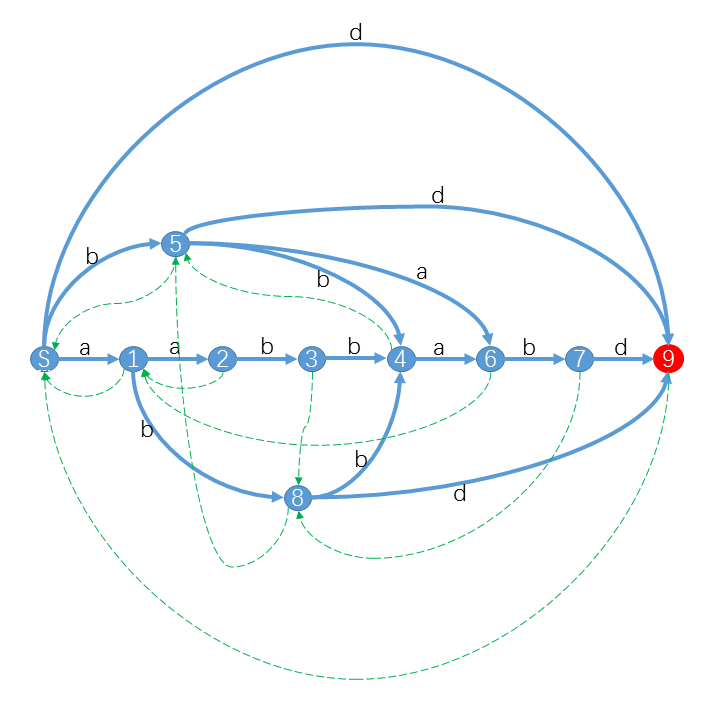
后缀自动机的DAG部分

后缀的\(Dag\)(有向无环图)部分由状态和转移函数构成，

状态表示原字符串若干个匹配结束位置相同的子串，这个结束位置的集合称为\(endpos\)

我们把这些子串中最长的记录下来，称为\(len\)

转移函数\(trans\)指原状态所包含的子串可以继续往后添加使得自动机识别的字符

由SAM的性质，沿着SAM的转移所得到的字符串一定是原串的一个子串

因此SAM的DAG部分相当于把原串的所有字串所构成的trie树压缩了

后缀自动机的Parent树部分

后缀的Parent树部分由Suffix-Links组成

沿着Suffix-Links走，我们能走到固定前缀的所有后缀

因此Parent树就是原串反串的后缀树

利用这个性质我们可以求出两后缀的\(LCP\)等经典后缀数组问题

我们记录一个\(fa\)数组表示Parent树中每个节点的父亲是谁

可以知道这个\(fa\)指针可以作为trie树中的fail指针

因此我们可以在SAM中匹配一个串中是否存在给定串的子串

Parent树中每个状态的\(sz\)实际表示\(|endpos|\)

将每个状态按照\(len\)递增的顺序进行遍历，那么遍历状态的顺序实际dfs Parent树和DAG的顺序

因此我们基数排序后按照\(len\)递减的顺序遍历可以求出\(sz\)

for(RG int i=1;i<=tot;i++)t[len[i]]++;
for(RG int i=1;i<=tot;i++)t[i]+=t[i-1];
for(RG int i=1;i<=tot;i++)a[t[len[i]]--]=i;
for(RG int i=tot;i;i--)sz[fa[a[i]]]+=sz[a[i]];

上面的定义看看有个印象就好,如果觉得fdf太菜不知所云的话就继续往下看吧

如何构建SAM

[推荐教程和例子]一开始就是在\(hihocoder\)上学的。

首先我们再次说明一条性质:

沿着某个节点的\(fail\)指针一直走,我们可以找到这个节点表示的最长字串的所有后缀,且其长度递减

考虑增量构造,初始我们有一个节点,表示空串。

假设我们已经建好了字符串\(s\)的\(SAM\),接下来我们要在末尾加入字符\(c\)。

以下过程建议大家手玩一下。

begin:增量构造

首先我们肯定无法在原串中找到一个表示字符串\(s+c\)的状态节点,因此我们必须建立一个新的节点\(cur\)来表示这个状态。

然后,我们考虑在\(SAM\)中加入字符串\(s+c\)的所有后缀。

而\(s+c\)的所有后缀一定是由\(s\)的所有后缀拼上\(c\)所构成的。

因此,我们从原来表示字符串\(s\)的节点\(last\)开始沿着\(fail\)数组向上走。

Case 1

假设此时经过某个节点\(u\),它能够表示的最长字符串为\(w\),显然有\(w\)是\(s\)的后缀。

如果\(u\)没有字符\(c\)的转移,那么说明\(w+c\)在\(s\)中是不存在的。

于是直接向\(u\)中添加\(trans(u,c)\)即可。

如果这样直接走到了初始节点,那么我们把\(cur\)的\(fail\)指针直接指向初始节点即可。

Case 2

继续沿着\(fail\)指针走,我们发现我们碰到了一个节点\(u\),并停了下来,因为它已经包含\(trans(u,c)\)的转移。

这说明\(w+c\)在\(s\)中存在,我们记\(v=trans(u,c)\)。

此时我们知道因为\(w+c\)为\(s+c\)的后缀,\(w+c\)表示状态的\(endpos\)集合需要增加。

但是我们的节点\(v\)不一定仅表示\(w+c\)这一个状态;

它可能包含\(p+c\)这个字符串,其中\(w\)为\(p\)的后缀,也可能包含\(q+c\)这个字符串,其中\(q\)为\(w\)的后缀。

因为\(q\)同时也为\(s\)的后缀,表示\(q+c\)的节点的\(endpos\)集合同样要增加,因此仍然可以把表示\(q+c\)的状态和表示\(w+c\)的状态放在一起;

但由于\(w\)是满足\(w+c\)在\(s\)内的最长串,因此表示\(p+c\)的节点的\(endpos\)集合不会增加;

而\(p+c\)和\(q+c\)现在仍然由节点\(v\)表示;这就产生了矛盾。

Case 2-1

我们对于\(p+c\)这样的字符串是否被\(v\)表示进行分类。

如果\(v\)没有表示\(p+c\)这样的字符串,那么\(v\)仍然是符合要求的;

这种情况的判断条件是\(len[v]=len[u]+1\)。

Case 2-2

如果\(v\)表示了\(p+c\)这样的字符串,那么\(p+c\)和\(w+c\)的\(endpos\)集合会不相同;

这种情况的判断条件是\(len[v]>len[u]+1\)。于是我们要进行分裂状态。

将\(v\)拆成\(v'\)和\(clone\)两个节点;

\(v'\)表示\(p+c\)这一类长度\(>len[u]+1\)的字符串,即\(len[v']=len[v]\);

\(clone\)表示\(q+c\)这一来长度\(\le len[u]+1\)的字符串,即\(len[clone]=len[u]+1\)。

为了不影响之前的转移,\(trans(v')=trans(clone)=trans(v)\)。

因为\(clone\)表示的字符串都是\(v'\)表示的字符串的后缀,

那么\(fail[v']=clone,fail[clone]=fail[v]\),原来\(fail\)指向\(v\)的节点现在指向\(v'\)。

原来\(trans\)指向\(v\)的状态呢?

注意到\(len[x]\)同时表示从初始节点到达\(x\)的最长路,那么原来指向\(v\)的节点中,\(len\le len[u]\)的节点自然指向\(clone\),\(>len[u]\)的节点指向\(v'\)。

而要找到\(len\le len[u]\)且表示的字符串为\(w\)的后缀的节点,只须沿着\(u\)的\(fail\)指针继续向上跳即可。

一个小小的总结

构建\(SAM\)使用增量法,初始使用一个节点表示空串,每次在\(s\)的\(SAM\)的基础上,新加一个字符\(c\)。

新建一个状态\(cur\),从表示\(s\)的状态\(last\)开始沿着\(fail\)指针向上走,在碰到一个节点\(u\)存在字符\(c\)的转移之前,将这些节点关于字符\(c\)的转移指向\(cur\),\(len[cur]=len[last]+1\)。

当碰到一个节点\(u\)满足\(trans(u,c)=v\)时,分两种情况讨论:

\(len[v]=len[u]+1\),此时只须将\(cur\)的\(fail\)指针指向\(v\)即可。

\(len[v]>len[u]+1\),此时复制一个新状态\(clone\),\(clone\)得到\(v\)的\(trans\)和\(fail\)指针。

令\(fail[v]=clone\),\(len[clone]=len[u]+1\),并再沿着\(u\)的\(fail\)指针向上走,每当\(trans(u,c)==v\)时改变为\(clone\)。

最后,将\(last\)置为\(cur\)即可。

• 代码

il void extend(int c){
    int cur=++tot,u=lst;len[cur]=len[u]+1;
    while(u&&!tr[u][c])tr[u][c]=cur,u=fa[u];
    if(!u)fa[cur]=1;
    else{
        int v=tr[u][c];
        if(len[v]==len[u]+1)fa[cur]=v;
        else{
            int clone=++tot;len[clone]=len[u]+1;
            memcpy(tr[clone],tr[v],sizeof(tr[clone]));
            fa[clone]=fa[v];fa[v]=fa[cur]=y;
            while(u&&tr[u][c]==v)tr[u][c]=clone,u=fa[u];
        }
    }
    lst=cur;
}