POJ 3845 Fractal（计算几何の旋转缩放）

Description

Fractals are really cool mathematical objects. They have a lot of interesting properties, often including: 
1. fine structure at arbitrarily small scales; 
2. self-similarity, i.e., magnified it looks like a copy of itself; 
3. a simple, recursive definition. 
Approximate fractals are found a lot in nature, for example, in structures such as clouds, snow flakes, mountain ranges, and river networks. 

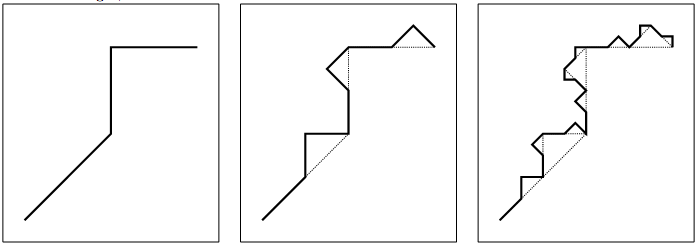
In this problem, we consider fractals generated by the following algorithm: we start with a polyline, i.e., a set of connected line segments. This is what we call a fractal of depth one (see leftmost picture). To obtain a fractal of depth two, we replace each line segment with a scaled and rotated version of the original polyline (see middle picture). By repetitively replacing the line segments with the polyline, we obtain fractals of arbitrary depth and very fine structures arise. The rightmost picture shows a fractal of depth three. 
The complexity of an approximate fractal increases quickly as its depth increases. We want to know where we end up after traversing a certain fraction of its length.

Input

The input starts with a single number c (1 <= c <= 200) on one line, the number of test cases. Then each test case starts with one line with n (3 <= n <= 100), the number of points of the polyline. Then follow n lines with on the ith line two integers xi and yi ( -1 000 <= xi, yi <= 1 000), the consecutive points of the polyline. Next follows one line with an integer d (1 <= d <= 10), the depth of the fractal. Finally, there is one line with a floating point number f (0 <= f <= 1), the fraction of the length thatis traversed. 
The length of each line segment of the polyline is smaller than the distance between the first point (x1, y1) and the last point (xn, yn) of the polyline. The length of the complete polyline is smaller than twice this distance.

Output

Per test case, the output contains one line with the coordinate where we end up. Format it as (x,y), with two floating point numbers x and y. The absolute error in both coordinates should be smaller than 10^-6.

 

题目大意：给一条折线，每一次操作把这条折线的所有线段变换成跟这条折线的相同形状，重复d次。问此时从头到尾走全长的f（0≤f≤1），将停在哪个点上。

思路：首先，设t = 这条折线的长度 / 头到尾的直线距离

那么这条线段变换成折线的时候，长度就会增大 t 倍

变换d次，长度就会增大 t^d 倍

那么，每一条线段变换后的长度都是可以直接求出来的，如果这条线段和之前的线段的长度加起来不到 全长 * f，就可以直接跳过

接下来就是缩放和旋转的细节，这些就不讲了，可以直接看代码，最下面分割线下的就是主要代码

为了代码简单化，几乎大部分都变成函数了

PS：这题虽然不难，但是花了大量的时间……最主要的原因是一开始看错题了……

 

代码（0MS）：

 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #include <cmath>
 using namespace std;

 const int MAXN = ;
 const double EPS = 1e-;
 const double PI = acos(-1.0);//3.14159265358979323846
 const double INF = ;

 inline int sgn(double x) {
     return (x > EPS) - (x < -EPS);
 }

 struct Point {
     double x, y, ag;
     Point() {}
     Point(double x, double y): x(x), y(y) {}
     void read() {
         scanf("%lf%lf", &x, &y);
     }
     bool operator == (const Point &rhs) const {
         return sgn(x - rhs.x) ==  && sgn(y - rhs.y) == ;
     }
     bool operator < (const Point &rhs) const {
         if(y != rhs.y) return y < rhs.y;
         return x < rhs.x;
     }
     Point operator + (const Point &rhs) const {
         return Point(x + rhs.x, y + rhs.y);
     }
     Point operator - (const Point &rhs) const {
         return Point(x - rhs.x, y - rhs.y);
     }
     Point operator * (const double &b) const {
         return Point(x * b, y * b);
     }
     Point operator / (const double &b) const {
         return Point(x / b, y / b);
     }
     double length() {
         return sqrt(x * x + y * y);
     }
     Point unit() {
         return *this / length();
     }
     void print() {
         printf("%.10f %.10f\n", x, y);
     }
 };
 typedef Point Vector;

 double dist(const Point &a, const Point &b) {
     return (a - b).length();
 }

 double cross(const Point &a, const Point &b) {
     return a.x * b.y - a.y * b.x;
 }
 //ret >= 0 means turn left
 double cross(const Point &sp, const Point &ed, const Point &op) {
     return sgn(cross(sp - op, ed - op));
 }

 double area(const Point& a, const Point &b, const Point &c) {
     return fabs(cross(a - c, b - c)) / ;
 }
 //counter-clockwise
 Point rotate(const Point &p, double angle, const Point &o = Point(, )) {
     Point t = p - o;
     double x = t.x * cos(angle) - t.y * sin(angle);
     double y = t.y * cos(angle) + t.x * sin(angle);
     return Point(x, y) + o;
 }

 struct Seg {
     Point st, ed;
     double ag;
     Seg() {}
     Seg(Point st, Point ed): st(st), ed(ed) {}
     void read() {
         st.read(); ed.read();
     }
     void makeAg() {
         ag = atan2(ed.y - st.y, ed.x - st.x);
     }
 };
 typedef Seg Line;

 //ax + by + c > 0
 Line buildLine(double a, double b, double c) {
     if(sgn(a) ==  && sgn(b) == ) return Line(Point(sgn(c) >  ? - : , INF), Point(, INF));
     if(sgn(a) == ) return Line(Point(sgn(b), -c/b), Point(, -c/b));
     if(sgn(b) == ) return Line(Point(-c/a, ), Point(-c/a, sgn(a)));
     if(b < ) return Line(Point(, -c/b), Point(, -(a + c) / b));
     else return Line(Point(, -(a + c) / b), Point(, -c/b));
 }

 void moveRight(Line &v, double r) {
     double dx = v.ed.x - v.st.x, dy = v.ed.y - v.st.y;
     dx = dx / dist(v.st, v.ed) * r;
     dy = dy / dist(v.st, v.ed) * r;
     v.st.x += dy; v.ed.x += dy;
     v.st.y -= dx; v.ed.y -= dx;
 }

 bool isOnSeg(const Seg &s, const Point &p) {
     return (p == s.st || p == s.ed) ||
         (((p.x - s.st.x) * (p.x - s.ed.x) <  ||
           (p.y - s.st.y) * (p.y - s.ed.y) < ) &&
          sgn(cross(s.ed, p, s.st) == ));
 }

 bool isIntersected(const Point &s1, const Point &e1, const Point &s2, const Point &e2) {
     return (max(s1.x, e1.x) >= min(s2.x, e2.x)) &&
         (max(s2.x, e2.x) >= min(s1.x, e1.x)) &&
         (max(s1.y, e1.y) >= min(s2.y, e2.y)) &&
         (max(s2.y, e2.y) >= min(s1.y, e1.y)) &&
         (cross(s2, e1, s1) * cross(e1, e2, s1) >= ) &&
         (cross(s1, e2, s2) * cross(e2, e1, s2) >= );
 }

 bool isIntersected(const Seg &a, const Seg &b) {
     return isIntersected(a.st, a.ed, b.st, b.ed);
 }

 bool isParallel(const Seg &a, const Seg &b) {
     return sgn(cross(a.ed - a.st, b.ed - b.st)) == ;
 }

 //return Ax + By + C =0 's A, B, C
 void Coefficient(const Line &L, double &A, double &B, double &C) {
     A = L.ed.y - L.st.y;
     B = L.st.x - L.ed.x;
     C = L.ed.x * L.st.y - L.st.x * L.ed.y;
 }
 //point of intersection
 Point operator * (const Line &a, const Line &b) {
     double A1, B1, C1;
     double A2, B2, C2;
     Coefficient(a, A1, B1, C1);
     Coefficient(b, A2, B2, C2);
     Point I;
     I.x = - (B2 * C1 - B1 * C2) / (A1 * B2 - A2 * B1);
     I.y =   (A2 * C1 - A1 * C2) / (A1 * B2 - A2 * B1);
     return I;
 }

 bool isEqual(const Line &a, const Line &b) {
     double A1, B1, C1;
     double A2, B2, C2;
     Coefficient(a, A1, B1, C1);
     Coefficient(b, A2, B2, C2);
     return sgn(A1 * B2 - A2 * B1) ==  && sgn(A1 * C2 - A2 * C1) ==  && sgn(B1 * C2 - B2 * C1) == ;
 }

 struct Poly {
     int n;
     Point p[MAXN];//p[n] = p[0]
     void init(Point *pp, int nn) {
         n = nn;
         for(int i = ; i < n; ++i) p[i] = pp[i];
         p[n] = p[];
     }
     double area() {
         if(n < ) return ;
         double s = p[].y * (p[n - ].x - p[].x);
         for(int i = ; i < n; ++i)
             s += p[i].y * (p[i - ].x - p[i + ].x);
         return s / ;
     }
 };

 void Graham_scan(Point *p, int n, int *stk, int &top) {//stk[0] = stk[top]
     sort(p, p + n);
     top = ;
     stk[] = ; stk[] = ;
     for(int i = ; i < n; ++i) {
         while(top && cross(p[i], p[stk[top]], p[stk[top - ]]) >= ) --top;
         stk[++top] = i;
     }
     int len = top;
     stk[++top] = n - ;
     for(int i = n - ; i >= ; --i) {
         while(top != len && cross(p[i], p[stk[top]], p[stk[top - ]]) >= ) --top;
         stk[++top] = i;
     }
 }
 //use for half_planes_cross
 bool cmpAg(const Line &a, const Line &b) {
     if(sgn(a.ag - b.ag) == )
         return sgn(cross(b.ed, a.st, b.st)) < ;
     return a.ag < b.ag;
 }
 //clockwise, plane is on the right
 bool half_planes_cross(Line *v, int vn, Poly &res, Line *deq) {
     int i, n;
     sort(v, v + vn, cmpAg);
     for(i = n = ; i < vn; ++i) {
         if(sgn(v[i].ag - v[i-].ag) == ) continue;
         v[n++] = v[i];
     }
     int head = , tail = ;
     deq[] = v[], deq[] = v[];
     for(i = ; i < n; ++i) {
         if(isParallel(deq[tail - ], deq[tail]) || isParallel(deq[head], deq[head + ]))
             return false;
         while(head < tail && sgn(cross(v[i].ed, deq[tail - ] * deq[tail], v[i].st)) > )
             --tail;
         while(head < tail && sgn(cross(v[i].ed, deq[head] * deq[head + ], v[i].st)) > )
             ++head;
         deq[++tail] = v[i];
     }
     while(head < tail && sgn(cross(deq[head].ed, deq[tail - ] * deq[tail], deq[head].st)) > )
         --tail;
     while(head < tail && sgn(cross(deq[tail].ed, deq[head] * deq[head + ], deq[tail].st)) > )
         ++head;
     if(tail <= head + ) return false;
     res.n = ;
     for(i = head; i < tail; ++i)
         res.p[res.n++] = deq[i] * deq[i + ];
     res.p[res.n++] = deq[head] * deq[tail];
     res.n = unique(res.p, res.p + res.n) - res.p;
     res.p[res.n] = res.p[];
     return true;
 }

 /*******************************************************************************************/

 Point p[MAXN], ans;
 double f[], sum[MAXN];
 double len, sqrt2 = sqrt();
 int c, n, d;

 void dfs(const Point &a, const Point &b, double len, int dep) {
     if(dep == ) {
         ans = (b - a) * len / dist(a, b) + a;
     } else {
         for(int i = ; i < n; ++i) {
             if(sgn(sum[i] * dist(a, b) / dist(p[], p[n - ]) * f[dep] - len) < ) continue;
             double angle1 = atan2(p[n - ].y - p[].y, p[n - ].x - p[].x);
             double angle2 = atan2(b.y - a.y, b.x - a.x);
             Point o = rotate(p[i - ], angle2 - angle1, p[]);
             o = (o - p[]) * dist(a, b) / dist(p[], p[n - ]) + a;
             Point t = rotate(p[i], angle2 - angle1, p[]);
             t = (t - p[]) * dist(a, b) / dist(p[], p[n - ]) + a;
             dfs(o, t, len - sum[i - ] * f[dep] * dist(a, b) / dist(p[], p[n - ]), dep - );
             return ;
         }
     }
 }

 void solve() {
     sum[] = ;
     for(int i = ; i < n; ++i) sum[i] = sum[i - ] + dist(p[i - ], p[i]);
     f[] = ;
     double tmp = sum[n - ] / dist(p[], p[n - ]);
     for(int i = ; i <= d; ++i) f[i] = f[i - ] * tmp;
     dfs(p[], p[n - ], len * sum[n - ] * f[d], d);
 }

 int main() {
     scanf("%d", &c);
     while(c--) {
         scanf("%d", &n);
         for(int i = ; i < n; ++i) p[i].read();
         scanf("%d%lf", &d, &len);
         solve();
         printf("(%.10f,%.10f)\n", ans.x, ans.y);
     }
 }