最短路径算法（II）

什么？？你问我为什么不在一篇文章写完所有方法？？
Hmm…其实我是想的，但是博皮的加载速度再带上文章超长图片超多的话…
可能这辈子都打不开了吧…

上一篇：Floyed and dijkstra

福特算法(Bellman-Ford)

适用范围及时间复杂度

单源最短路径算法，可处理负边权，但，无法处理负回路的情况。时间复杂度O（NE）

N：顶点数，E：边数

核心思想

松弛计算。什么是松弛计算？你戳…

……

aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQEAYABgAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCABLAHkDASIAAhEBAxEB/8QAGwAAAQUBAQAAAAAAAAAAAAAABAECAwUGAAf/xAA0EAACAQIFAgUCBQMFAQAAAAABAhEAAwQFEiExQVEGEyJhgQdxFBVSkaEjMsEkM2Kx0fD/xAAZAQACAwEAAAAAAAAAAAAAAAABAgADBAX/xAAeEQACAgIDAQEAAAAAAAAAAAAAAQIRAyESMUEEE//aAAwDAQACEQMRAD8A9jVvVtx3p5bSDBioIiBzSajwP5rKaOKsl1g7dKY5gcTUbOFBnniq18U7XCupo6CYqyMOSsaqLRSdQk0+Y6TvVTbvsyn1sT71ML7MNmam4UQPF0ByBE01rg56dTQBusr6zJn3pxuOUJNNxXgtMP1+mBUb3CIKn5NCG8zCCNgOZpfMIQf3Ek1NJEDVcORuQfYxXOxUHqBzQAuMHEGD3miEYEEMx95ocd6CokjXwGAIO1R3GU7jrUVwjVKk+wpS5CgRzRpJ6J0cX5PNJ5x7fxTC0UkjvTp0GyxVgwESYprGH9Q27UwHTEGKT+/cgmsozobdILdKqCy6mLbCatLhPl7c96pTaZ7rCSQDWjElQrC7WkhjbYEU9DDDeCeYoYI8BVAAqewrqPWAOs1HrsDPPs5+qTYfH42xlmVHFYfCObVzFPc0gPuJC9QCPmKprP1ixqZYbf4FMTjS5/qPCWwvTYc9e1Wf1C8H5dgMpzDOcBh7qYzF3LaFEc6CXb1Np4E/5rGZX4LbGYmyLz/6a0ZvXQ49Z/QgB2H/ACPPSnlmilpFmPBKbs0WWfWTFWrrfm+VW3tNGlsKdBX4YkH+KtLP1ZxmJuOmAyUY5jbL27dskG2o3Jc78DmAN6yPifw1hr13GY7LMXaFxE8y7hAQdlG5EcbdDVL4NwOY5tm13AZabpF61/X0PoJs6hq9XQcUynGUbEy4pY57Pd/CHie14ryH8y/Dmw63DbuWydQVhvse0EVfC4XRtO3361UZF4fy/wANZYuXYBXFoOXZnaWZj1J+P4qwuBliIj71nclegonsmDIXpTrryAY3/ah7b+XB1bE0rnYbyDNGPdga2cXHE7e9d5g70yOvekn7ftTgLC2waQTxS6ih5371BbMKBNOJBX7jasxY0I9wlTHNU6vqJMmZqy/UBxVWWXzCQI36VqxdCMIS4QNzvRFt1uRJiKEUhuaJsQzRxUyLRDGfU3HqtjB4A6ghW5iGaCQSBCgx7z+1Z/K7NnSccLrXnuqQCLYB0mNjpHqjoTvWw8d4Ow35dj7l5rYtscO0Ho3qB+CvPT7Vh8VawuX3FvG0L2FuqNBQalFzrAGw1DfbqDWZpt0dT5XFY9kOMVMDhsRg7N4lb4aQFCrbEcAAVf8A0uyW1hr2OzexYZLVy2tmxcMgOJliPbZR96rrWQ3r1izmmK8lsLeYCzaW6Ha+ei7TC7ereQAetajwtnFyxf8AyXF3FbRAw1wKFlSJ0QOIgx7COlXRxuMSr7sn6vlBVFGy1qRzHemtcXed4HFQsjqoaRv2FcghZUye3UVXS9MIt0qEAMyfimo+u2omYmor5lxMn27UqMotDcRPMVckq0g+k2ojma6V/wDhUJfptS6l7VCXENZt9+OgplxxpADEe1IxIWD196EYknfp0qhKyPQWLgCxNVRhbhAbYHaiC5j44quFw64IH7VpwrQrCw4USePap7FxmYAEATQAYSF6Ci8OfVI71MvRKozvjF1vZ1luHJugpZuXA6baGkAGe5AYdqyuEyvDscdltzEXglx/NNnY+ljswJEiSN4iDWr8TejP8MxO17CMJ90ef+nrFX8wXB+LPPuQLYCYYtO2kyWJ+xKn4oWmjp4qUIhduzayPBYryterCgsoBkMrEeuONUAgkdqtTZYYJpIXEhNYujlHHqEewMVDm+CGIwd5lcpdS22llO5HVT3Bj/NCvmwu5W95UZLtxjZFtjJDnYb/AGM/aj2rDNqEZJnp+CxD4rLsLfuKFe9ZS4R2JUEj+aY6w/JBHEVKB5NhLSAabahPgCKGZmBg/MVTE5rEuagYLfNNRvRt0NOZYA32NMU+kg7DvVl6Qno7VPuZpPmk0g9KWPcftQWw0FI+rpt96hdtJO/vTQSJjpxXcsJ7VnToa77Gglu8zQ64Egkh9pmjF5HxTgNmPWnU34KlbBFwpBEsCO9SpZ0Ns3HtUs+meuqKcm4AqObYyVgWZ5Ic1t2NN/yL1li1t9GuJEEEHkHb9hWXzL6a43MhdfEZrhy7IqrowxVVIaSYB3mTNb+2ACIoi5/t/FLylYym10YrCeDcRh8s/B3cwW7CaFuG2dQWIg9+v8UJf8EacSLi4xAmlRp0HdgV9XP6VC1t25FB4kkHbvTKTJLJJ6bJrjE7jk9JpgwpeGDqWkejeT2+T0FK5IMChXJEwSNo/g0Ylcm6JndCAdSkTHO9NkOgKRHTfmozaRyiMCVEbSaccPaBYhY4PJ7H/wAoibsRnRAdTqAO5rtfuKj8pQo/u9QAPqNL5SfppkMr9P/ZAA==" alt="" />

好吧我说…

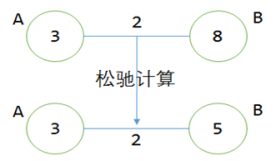松弛计算之前,点B的值是8,但点A的值加上边上的权重2,得到点B的值是5,5<8,更新B为5。这个过程的意义是:找到了一条通向B更短的路线,且该路线先经过A,然后通过权重为2的边,到达点B。

当然，也会存在另一种情况：

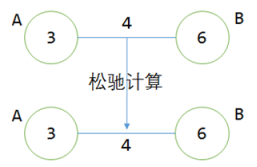在进行松弛计算之前,点B的值是6,点A加上点边上的权值4得到7>6,表示没有找到通向B点更短的路线,故B不需要更新。
这也就诠释了为什么算法不可以处理负权回路的情况。

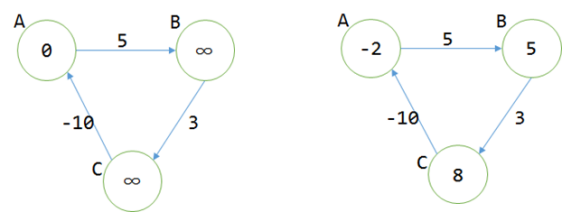
使用松弛之后，发现程序陷入死循环。

代码实现

不难发现，在使用算法前，我们要去检验负权回路。我们需要不断地迭代以求解。

初始化

首先我们需要一个边集数组，暂定u表示起点，v表示终点，w表示权。而这个数组的长度为边的数量。

顶点数*（顶点数-1）/2。

什么？你不知道什么是边集数组？

 边集数组
  边集数组是利用一维数组存储图中所有边的一种图的表示方法。
  该数组中所存储的元素个数要大于等于图中所有的边数。
  每个元素用来存储图一条边起点,终点和权值。
  struct edge{int s,e;double w;}edges[maxn*(maxn-)/];
  特别注意的是:如果是无向图,则边的数量=顶点数量*(顶点数量-)/,加边函数为:
      void addEdges(int u,int v,double w){
      edges[++idx].s=u;edges[idx].e=v;edges[idx].w=w;
     edges[++idx].e=u;edges[idx].s=v;edges[idx].w=w;
 }
 而在枚举边的时候,需要枚举idx条边。
 定义边集数组时,特别要注意取值范围
 边集数组是针对边的,如果题目给定了边的数量为n
 ,那么在无向邻接矩阵中,边集数组要定义为2*n+,
 必须考虑来回。如果题目只给定了顶点数p,没有给定边数,
 则边集数组的取值为:p*(p-)/

因为是无向图，算法第一层循环枚举点，第二层枚举边，所以加边函数的定义应是无向图的方法。

算法核心

void bellman(){
    while(--n){
        bool b=false;
        for(int j=;j<=idx;j++){
            if(dis[edges[j].e]>dis[edges[j].s]+edges[j].w){
                dis[edges[j].e]=dis[edges[j].s]+edges[j].w;
                b=true;
            }
        }
        if(!b){
            break;
        }
    }
} 

----------7.22 Update

学个A*不知道扒出来了我多少学错了的东西…这篇里面提到了最基本的福特算法，但是有一个队列优化没有补充。我一直误以为SPFA是福特算法的别称，在这里做出纠正顺便优化一下之前乱七八糟的写法。

SPFA（队列优化的Bellman-Ford）

仅仅在大陆流行叫这个优化SPFA。优化过后，在随机数据的表现情况为O（KE），K是一个较小的常数。在特殊构造中，有可能被退化成O（NE）。

优化思想是：

1.建立一个队列，最初队列中只有一个起点1

2.取出队首节点x，扫描他的所有出边(x,y,z)。如果有Dis[y]>Dis[x]+z，则用后者更新前者。同时，若y不在队列中，将y入队

3.重复以上步骤，直至队列为空。

这个队列避免了福特算法中对不需要进行扩展的节点的冗余扫描。

void spfa()
{
    memset(Distance,0x3f,sizeof(Distance));
    memset(Vist,,sizeof(Vist));
    Distance[]=;
    Vist[]=;
    q.push();
    while(q.size())
    {
        int x=q.front();
        q.pop();
        Vist[x]=;
        for(int i=head[x]; i; i=Edges[i].Next)
        {
            int y=Edges[i].End,z=Edges[i].Val;
            if(Distance[y]>Distance[x]+z)
            {
                Distance[y]=Distance[x]+z;
                if(!Vist[y])
                {
                    q.push(y),Vist[y]=;
                }
            }
        }
    }
}