[学习笔记]min-max容斥
min-max容斥
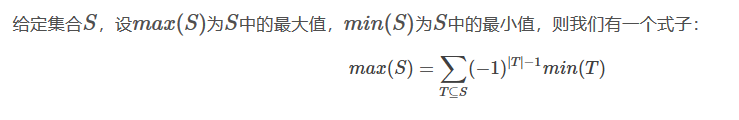
就是max(a,b)=min(a)+min(b)-min(a,b)
max(a,b,c)=a+b+c-min(a,b)-min(a,c)-min(b,c)+min(a,b,c)
....
为什么这样做？
有的时候min要好算很多
期望的线性
所以可以直接套期望
然后例题：
[HAOI2015]按位或
推广
from：在Ta的博客查看
max_k(S)表示S中第k大
依然可以套期望：
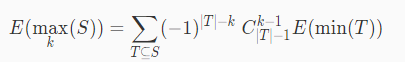
[学习笔记]min-max容斥的更多相关文章
- 【学习笔记】Min-max 容斥
经常和概率期望题相结合. 对于全序集合 \(S\),有: \[\max S=\sum\limits_{T\subseteq S,T\not=\varnothing}(-1)^{\vert T\vert ...
- 快速沃尔什变换 (FWT)学习笔记
证明均来自xht37 的洛谷博客 作用 在 \(OI\) 中,\(FWT\) 是用于解决对下标进行位运算卷积问题的方法. \(c_{i}=\sum_{i=j \oplus k} a_{j} b_{k} ...
- min-max 容斥
$\min - \max$ 容斥 Part 1 对于简单的$\min - \max$容斥有一般形式,表达为:$\max(S)=\sum\limits_{T\subseteq S}(-1)^{|T|-1 ...
- Min-max 容斥与 kth 容斥
期望的线性性: \[E(x+y)=E(x)+E(y) \] 证明: \[E(x+y)=\sum_i \sum_j(i+j)*P(i=x,j=y) \] \[=\sum_i\sum_ji*P(i=x,j ...
- min-max容斥学习笔记
min-max容斥学习笔记 前置知识 二项式反演 \[ f(n)=\sum_{i=0}^n\binom{n}{i}g(i)\Leftrightarrow g(n)=\sum_{i=0}^n(-1)^{ ...
- [总结] Min-Max容斥学习笔记
min-max 容斥 给定集合 \(S\) ,设 \(\max(S)\) 为 \(S\) 中的最大值,\(\min(S)\) 为 \(S\) 中的最小值,则: \[\max(S)=\sum_{T\in ...
- MinMax 容斥 学习笔记
基本形式 \[ \max(S) = \sum_{T\subseteq S, T \neq \varnothing} (-1)^{|T|-1}\min(T) \] 证明 不提供数学证明. 简要讲一下抽象 ...
- $Min\_25$筛学习笔记
\(Min\_25\)筛学习笔记 这种神仙东西不写点东西一下就忘了QAQ 资料和代码出处 资料2 资料3 打死我也不承认参考了yyb的 \(Min\_25\)筛可以干嘛?下文中未特殊说明\(P\)均指 ...
- [模板] 容斥原理: 二项式反演 / Stirling 反演 / min-max 容斥 / 子集反演 / 莫比乌斯反演
//待更qwq 反演原理 二项式反演 若 \[g_i=\sum_{j=1}^i {\binom ij} f_j\] , 则有 \[ f_i=\sum_{j=1}^i (-1)^{i-j} {i \ch ...
随机推荐
- APP上下左右滑动屏幕的处理
#获得机器屏幕大小x,y driver = self.driver def getSize(): x = driver.get_window_size()['width'] y = driver.ge ...
- 使用python+selenium控制手工已打开的浏览器
我们可以利用Chrome DevTools协议.它允许客户检查和调试Chrome浏览器. 打开cmd,在命令行中输入命令: chrome.exe --remote-debugging-port=922 ...
- 运用GamePlayKit的GKEntity及GKComponent 的iOS游戏开发实例
GameplayKit是一个面向对象的框架,为构建游戏提供基础工具和技术. GameplayKit包含用于设计具有功能性,可重用架构的游戏的工具,以及用于构建和增强诸如角色移动和对手行为的游戏玩法特征 ...
- unable to access android sdk add-on list and SDK 更新镜像设置
前记 国内的网络呀,真是操蛋!!!!!! unable to access android sdk add-on list 在 Android Studio 安装目录 bin/idea.propert ...
- Java 集合学习--HashMap
一.HashMap 定义 HashMap 是一个基于散列表(哈希表)实现的键值对集合,每个元素都是key-value对,jdk1.8后,底层数据结构涉及到了数组.链表以及红黑树.目的进一步的优化Has ...
- 打包一个Docker镜像，让你的好友加载开启一个容器，并且每隔一秒输出hello，world到指定的文件中
一.两个脚本代码 Dockerfile FROM bash COPY . /usr/herui/ WORKDIR /usr/herui/ CMD [ "sh", "hel ...
- TensorFlow入门之MNIST最佳实践-深度学习
在上一篇<TensorFlow入门之MNIST样例代码分析>中,我们讲解了如果来用一个三层全连接网络实现手写数字识别.但是在实际运用中我们需要更有效率,更加灵活的代码.在TensorFlo ...
- How Does Batch Normalization Help Optimization?
1. 摘要 BN 是一个广泛应用的用于快速稳定地训练深度神经网络的技术,但是我们对其有效性的真正原因仍然所知甚少. 输入分布的稳定性和 BN 的成功之间关系很小,BN 对训练过程更根本的影响是:它让优 ...
- Java 单例模式探讨
以下是我再次研究单例(Java 单例模式缺点)时在网上收集的资料,相信你们看完就对单例完全掌握了 Java单例模式应该是看起来以及用起来简单的一种设计模式,但是就实现方式以及原理来说,也并不浅显哦. ...
- python函数中的位置参数、默认参数、关键字参数、可变参数区别
一.位置参数 调用函数时根据函数定义的参数位置来传递参数. #!/usr/bin/env python # coding=utf-8 def print_hello(name, sex): sex_d ...