【POJ1707】【伯努利数】Sum of powers

Description

A young schoolboy would like to calculate the sum


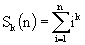
for some fixed natural k and different natural n. He observed that calculating i^k
for all i (1<=i<=n) and summing up results is a too slow way to
do it, because the number of required arithmetical operations increases
as n increases. Fortunately, there is another method which takes only a
constant number of operations regardless of n. It is possible to show
that the sum S_k(n) is equal to some polynomial of degree k+1 in the variable n with rational coefficients, i.e.,



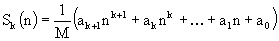
We require that integer M be positive and as small as possible. Under this condition the entire set of such numbers (i.e. M, a_k+1, a_k, ... , a₁, a₀)
will be unique for the given k. You have to write a program to find
such set of coefficients to help the schoolboy make his calculations
quicker.

Input

The input file contains a single integer k (1<=k<=20).

Output

Write integer numbers M, a_k+1, a_k, ... , a₁, a₀
to the output file in the given order. Numbers should be separated by
one space. Remember that you should write the answer with the smallest
positive M possible.

Sample Input

2

Sample Output

6 2 3 1 0

Source

Northeastern Europe 1997

【分析】

题意就是给出一个k,找一个最小的M使得中a[i]皆为整数.

这个涉及到伯努利数的一些公式，如果不知道的话基本没法做..

1. 伯努利数与自然数幂的关系：

2. 伯努利数递推式：

先通过递推式求得伯努利数，然后用1公式并将中间的(n+1) ^ i,变成n ^ i,后面再加上n ^ k，化进去就行了。

 /*
 宋代朱敦儒
 《西江月·世事短如春梦》
 世事短如春梦，人情薄似秋云。不须计较苦劳心。万事原来有命。
 幸遇三杯酒好，况逢一朵花新。片时欢笑且相亲。明日阴晴未定。
 */
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <cmath>
 #include <queue>
 #include <vector>
 #include <iostream>
 #include <string>
 #include <ctime>
 #define LOCAL
 const int MAXN =  + ;
 const double Pi = acos(-1.0);
 using namespace std;
 typedef long long ll;
 ll gcd(ll a, ll b){return b == ? a: gcd(b, a % b);}
 struct Num{
        ll a, b;//分数,b为分母
        Num(ll x = , ll y = ) {a = x;b = y;}
        void update(){
            ll tmp = gcd(a, b);
            a /= tmp;
            b /= tmp;
        }
        Num operator + (const Num &c){
            ll fz = a * c.b + b * c.a, fm = b * c.b;
            if (fz == ) return Num(, );
            ll tmp = gcd(fz, fm);
            return Num(fz / tmp, fm / tmp);
        }
 }B[MAXN], A[MAXN];
 ll C[MAXN][MAXN];

 void init(){
      //预处理组合数
      for (int i = ; i < MAXN; i++) C[i][] = C[i][i] = ;
      for (int i = ; i < MAXN; i++)
      for (int j = ; j < MAXN; j++) C[i][j] = C[i - ][j] + C[i - ][j - ];
      //预处理伯努利数
      B[] = Num(, );
      for (int i = ; i < MAXN; i++){
          Num tmp = Num(, ), add;
          for (int j = ; j < i; j++){
              add = B[j];
              add.a *= C[i + ][j];
              tmp = tmp + add;
          }
          if (tmp.a) tmp.b *= -(i + );
          tmp.update();
          B[i] = tmp;
      }
 }
 void work(){
      int n;
      scanf("%d", &n);
      ll M = n + , flag = , Lcm;
      A[] = Num(, );
      for (int i = ; i <= n + ; i++){
          if (B[n +  - i].a == ) {A[i] = Num(, );continue;}
          Num tmp = B[n +  - i];
          tmp.a *= C[n + ][i];//C[n+1][i] = C[n + 1][n + 1 - i]
          tmp.update();
          if (flag == ) Lcm = flag = tmp.b;
          A[i] = tmp;
      }
      A[n] = A[n] + Num(n + , );

      for (int i = ; i <= n + ; i++){
          if (A[i].a == ) continue;
          Lcm = (Lcm * A[i].b) / gcd(Lcm, A[i].b);
      }
      if (Lcm < ) Lcm *= -;
      M *= Lcm;
      printf("%lld", M);
      for (int i = n + ; i >= ; i--) printf(" %lld", A[i].a * Lcm / A[i].b);
 }

 int main(){

     init();
     work();
     //printf("%lld\n", C[5][3]);
     return ;
 }