POJ 2653 Pick-up sticks (判断线段相交)

Pick-up sticks

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 10330		Accepted: 3833

Description

Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.

Input

Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.

Output

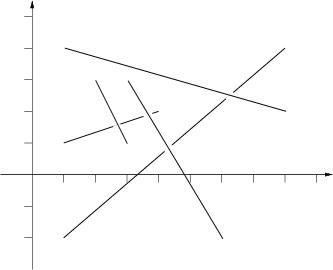
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.

The picture to the right below illustrates the first case from input.

Sample Input

5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0

Sample Output

Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.

Hint

Huge input,scanf is recommended.

直接暴力枚举每一条线段就行了,不过有个顺序问题,假设枚举第i个,如果往前枚举的话,排除前面的,这样会超时,如果判断第i个,从第i个往后枚举,不会超时

/*************************************************************************
    > File Name: poj_2653.cpp
    > Author:
    > Mail:
    > Created Time: 2015年04月02日 星期四 21时27分10秒
 ************************************************************************/

#include<iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = ;
bool vis[N];
struct point{
    double x, y;
};
struct Line{
    point Start, End;
};
Line line[N];
int n;
double Min(double a, double b)
{
    return a < b ? a : b;
}
double Max(double a, double b)
{
    return a > b ? a : b;
}
double get_direction(point a, point b, point c)
{
    point t1, t2;
    t1.x = c.x - a.x; t1.y = c.y - a.y;
    t2.x = b.x - a.x; t2.y = b.y - a.y;
    return (t1.x * t2.y - t2.x * t1.y);
}
bool on_segment(point a, point b, point c)
{
    double minx = Min(a.x, b.x);
    double maxx = Max(a.x, b.x);
    double miny = Min(a.y, b.y);
    double maxy = Max(a.y, b.y);
    return (c.x <= maxx && c.x >= minx && c.y <= maxy && c.y >= miny);
}
bool segment_intersect(point a, point b, point c, point d)//判断线段是否相交
{
    double d1 = get_direction(a, b, c);
    double d2 = get_direction(a, b, d);
    double d3 = get_direction(c, d, a);
    double d4 = get_direction(c, d, b);
    if (d1 * d2 <  && d3 * d4 < )
        return true;//规范相交
    //下面的四个都是非规范相交
    if (d1 ==  && on_segment(a, b, c))
        return true;
    if (d2 ==  && on_segment(a, b, d))
        return true;
    if (d3 ==  && on_segment(c, d, a))
        return true;
    if (d4 ==  && on_segment(c, d, b))
        return true;
    return false;
}
void check_segments(int m)
{
    for (int i = m + ; i < n; i++)
    {
        if (segment_intersect(line[i].Start, line[i].End, line[m].Start, line[m].End))
        {
            vis[m] = true;
            return;
        }
    }
}
int main()
{
    while (~scanf("%d", &n) && n)
    {
        memset(vis, false, sizeof(vis));
        for (int i = ; i < n; i++)
        {
            scanf("%lf %lf %lf %lf", &line[i].Start.x, &line[i].Start.y, &line[i].End.x, &line[i].End.y);
        }
        for (int i = ; i < n; i++)
            check_segments(i);
        printf("Top sticks: ");
        bool first = true;
        for (int i = ; i < n; i++)
        {
            if (!vis[i])
            {
                if (first)
                    first = false;
                else
                    printf(", ");
                printf("%d", i + );
            }
        }
        printf(".\n");
    }

    return ;
}