[LeetCode 119] - 杨辉三角形II(Pascal's Triangle II)

问题

给出一个索引k，返回杨辉三角形的第k行。

例如，给出k = 3，返回[1, 3, 3, 1]

注意：

你可以优化你的算法使之只使用O(k)的额外空间吗？

初始思路

首先来复习复习杨辉三角形的性质（来自wiki）：

1. 杨辉三角以正整数构成，数字左右对称，每行由1开始逐渐变大，然后变小，回到1。
2. 第行的数字个数为个。
3. 第行的第个数字为组合数。
4. 第行数字和为。
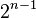5. 除每行最左侧与最右侧的数字以外，每个数字等于它的左上方与右上方两个数字之和（也就是说，第行第个数字等于第行的第个数字与第个数字的和）。这是因为有组合恒等式：。可用此性质写出整个杨辉三角形。

看到第2条和5条是不是发现和 [LeetCode 120] - 三角形(Triangle) 中的最终算法有点像？没错，这里可以使用类似的方法得出杨辉三角形中第k行的数据，而且更简单：

• 第1列和最后1列的数字永远为1
• 其他列如性质5所述，为上一行纵坐标j-1和纵坐标j的点之和

最终得出的只是用O(k)额外空间的代码如下：

 class Solution {
     public:
         std::vector<int> getRow(int rowIndex)
         {
             std::vector<int> columnInfo(rowIndex + );

             columnInfo[] = ;

             if(rowIndex == )
             {
                 return columnInfo;
             }

             columnInfo[] = ;

             for(int i = ; i < rowIndex + ; ++i)
             {
                 for(int j = i; j > ; --j)
                 {
                     if(j ==  || j == i)
                     {
                         columnInfo[j] = ;
                     }
                     else
                     {
                         columnInfo[j] = columnInfo[j - ] + columnInfo[j];
                     }
                 }
             }

             return columnInfo;
         }
 };

getRow

顺利通过Judge Small和Judge Large。

题外

根据杨辉三角形的性质3，我们也可以直接计算某行所有数的值。由于对称性，实际只需要计算前一半的列并将结果拷贝到后一半列即可。但是这种方法的问题是需要计算很大的阶乘，当行数达到一定大小时不做特殊处理就会溢出了。以下是一个示例，没做特殊处理，只是用int64_t保存中间结果。当输入为21时就会溢出了：

 class SolutionV2 {
     public:
         std::vector<int> getRow(int rowIndex)
         {
             std::vector<int> columnInfo(rowIndex + );

             nFactorial_ = ;

             for(int i = ; i <= rowIndex; ++i)
             {
                 nFactorial_ *= i;
             }

             columnInfo[] = ;
             columnInfo[rowIndex] = ;

             for(int i = ; i <= rowIndex / ; ++i)
             {
                 columnInfo[i] = CaculateCombination(rowIndex, i);
             }

             int left = ;
             int right = rowIndex - ;

             while(left < right)
             {
                 columnInfo[right] = columnInfo[left];
                 ++left;
                 --right;
             }

             return columnInfo;
         }

     private:
         int64_t CaculateCombination(int n, int k)
         {
             int64_t kFactorial = ;
             int64_t restFactorial = ;

             for(int i = ; i <= k; ++i)
             {
                 kFactorial *= i;
             }

             for(int i = ; i <= n - k; ++i)
             {
                 restFactorial *= i;
             }

             return nFactorial_ / (kFactorial * restFactorial);
         }

         int64_t nFactorial_;
     };

阶乘－有缺陷