PICK定理模板

PICK定理：

S=I+O/2-1

S为多边形面积，I多边形内部的格点，O是多边形边上的格点

其中边上格点求法：

假设两个点A（x1,y1),B（x2,y2）

线段AB间格点个数为gcd(abs(x1-x2),abs(y1-y2))-1

特判x1-x2==0 或者 y1-y2==0，则覆盖的点数为 y2-y1 或 x2-x1

POJ 2594

Triangle

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 5106		Accepted: 2210

Description

A lattice point is an ordered pair (x, y) where x and y are both integers. Given the coordinates of the vertices of a triangle (which happen to be lattice points), you are to count the number of lattice points which lie completely inside of the triangle (points on the edges or vertices of the triangle do not count).

Input

The input test file will contain multiple test cases. Each input test case consists of six integers x₁, y₁, x₂, y₂, x₃, and y₃, where (x₁, y₁), (x₂, y₂), and (x₃, y₃) are the coordinates of vertices of the triangle. All triangles in the input will be non-degenerate (will have positive area), and −15000 ≤ x₁, y₁, x₂, y₂, x₃, y₃ ≤ 15000. The end-of-file is marked by a test case with x₁ =  y₁ = x₂ = y₂ = x₃ = y₃ = 0 and should not be processed.

Output

For each input case, the program should print the number of internal lattice points on a single line.

Sample Input

0 0 1 0 0 1
0 0 5 0 0 5
0 0 0 0 0 0

Sample Output

0
6

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}

int main()
{
    int sum,area;
    int x1,Y1,x2,y2,x3,y3;
    while(scanf("%d%d%d%d%d%d",&x1,&Y1,&x2,&y2,&x3,&y3),x1||Y1||x2||y2||x3||y3)
    {
        area=abs(x1*y2+x2*y3+x3*Y1-x1*y3-x2*Y1-x3*y2)/;
        sum=gcd(abs(x1-x2),abs(Y1-y2))+gcd(abs(x2-x3),abs(y2-y3))+gcd(abs(x3-x1),abs(y3-Y1));
        printf("%d\n",area+-sum/);
    }
    return ;
}

POJ 1265

Area

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5112		Accepted: 2291

Description

Being well known for its highly innovative products, Merck would definitely be a good target for industrial espionage. To protect its brand-new research and development facility the company has installed the latest system of surveillance robots patrolling the area. These robots move along the walls of the facility and report suspicious observations to the central security office. The only flaw in the system a competitor抯 agent could find is the fact that the robots radio their movements unencrypted. Not being able to find out more, the agent wants to use that information to calculate the exact size of the area occupied by the new facility. It is public knowledge that all the corners of the building are situated on a rectangular grid and that only straight walls are used. Figure 1 shows the course of a robot around an example area.   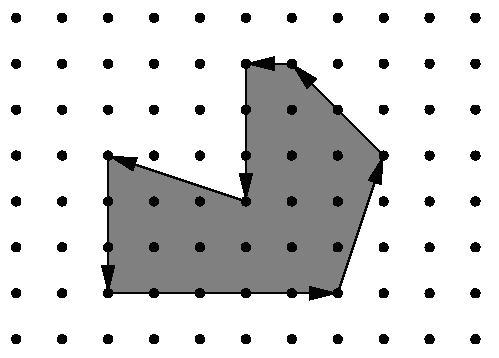Figure 1: Example area. You are hired to write a program that calculates the area occupied by the new facility from the movements of a robot along its walls. You can assume that this area is a polygon with corners on a rectangular grid. However, your boss insists that you use a formula he is so proud to have found somewhere. The formula relates the number I of grid points inside the polygon, the number E of grid points on the edges, and the total area A of the polygon. Unfortunately, you have lost the sheet on which he had written down that simple formula for you, so your first task is to find the formula yourself. 

Input

The first line contains the number of scenarios.  For each scenario, you are given the number m, 3 <= m < 100, of movements of the robot in the first line. The following m lines contain pairs 揹x dy�of integers, separated by a single blank, satisfying .-100 <= dx, dy <= 100 and (dx, dy) != (0, 0). Such a pair means that the robot moves on to a grid point dx units to the right and dy units upwards on the grid (with respect to the current position). You can assume that the curve along which the robot moves is closed and that it does not intersect or even touch itself except for the start and end points. The robot moves anti-clockwise around the building, so the area to be calculated lies to the left of the curve. It is known in advance that the whole polygon would fit into a square on the grid with a side length of 100 units. 

Output

The output for every scenario begins with a line containing 揝cenario #i:� where i is the number of the scenario starting at 1. Then print a single line containing I, E, and A, the area A rounded to one digit after the decimal point. Separate the three numbers by two single blanks. Terminate the output for the scenario with a blank line.

Sample Input

2
4
1 0
0 1
-1 0
0 -1
7
5 0
1 3
-2 2
-1 0
0 -3
-3 1
0 -3

Sample Output

Scenario #1:
0 4 1.0

Scenario #2:
12 16 19.0

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
using namespace std;

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;
}
int main()
{
    __int64 ans;
    int T,iCase=,n;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        int sx=,sy=,tx,ty;
        int on=,ans=;
        while(n--)
        {
            scanf("%d%d",&tx,&ty);
            int newx=sx+tx;
            int newy=sy+ty;
            ans+=sx*newy-sy*newx;
            sx=newx;
            sy=newy;
            on+=gcd(abs(tx),abs(ty));
        }
        int in=(ans-on+)/;
        printf("Scenario #%d:\n%d %d %.1f\n\n",iCase++,in,on,ans/2.0);
    }
    return ;
}