简单而粗暴的方法画任意阶数Bezier曲线

简单而粗暴的方法画任意阶数Bezier曲线

虽然说是任意阶数，但是嘞，算法原理是可以到任意阶数，计算机大概到100多阶就会溢出了

【Bezier曲线介绍】

【本文代码】

背景

在windows的OpenGL环境中，使用鼠标在屏幕上选点，并以点为基础画出Bezier曲线

• 初始化
• 鼠标操作
• 3阶以内Bezier曲线
• n阶Bezier曲线

初始化

创建窗口，初始化大小、显示模式、添加显示和鼠标等回调函数，设置背景颜色等。

完成之后，定义两个全局的int类型的vector 用于存储鼠标在窗口中选择的点。同时定义窗口的高度和宽度。

vector<int> x_loc = {};
vector<int> y_loc = {};
int height = 600;
int width  = 600;

• 定义画点函数

void drawPixel(double x, double y, int point_size)
{
	glViewport(0, 0, (GLsizei)width, (GLsizei)height);
	glEnable(GL_POINT_SMOOTH);
	glEnable(GL_BLEND);
	glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
	glPointSize(point_size);
	glBegin(GL_POINTS);
	glVertex2d(x, y);
	glEnd();
}

其中point_size为点的大小。

鼠标操作

OpenGL中存在鼠标点击、拖动等操作的回调函数，使用十分方便，调用即可。

我们定义在鼠标左键按下抬起后为一次屏幕选点，并将所选的点的坐标压入存储存储点的坐标的容器中。

void Mouse_hit(int button, int state, int x, int y)
{
	/// state == 1 mean button up
	/// state == 0 mean button down
	/// button == 0 mean left button
	/// button == 1 mean middle button
	/// button == 2 mean right button
	/// [x, y] is the location of mouse pointer
	if (button == 0 && state == 1)
	{
		x_loc.push_back(x);
		y_loc.push_back(y);
		cout << "point location: " << x_loc[x_loc.size() - 1] << " " << y_loc[y_loc.size() - 1] << endl;
	}
if (button == 2 && state == 1){
	   x_loc.clear();
	  y_loc.clear();
	  glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
	  glutSwapBuffers();
	  glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
	  glutSwapBuffers();
	  glutPostRedisplay();
	  cout<<" Clear Screen!"<<endl;
	}
	glutSwapBuffers();
	  glutPostRedisplay();
}

• 回调函数使用为

  glutMouseFunc(Mouse_hit);
  

• Mouse_hit函数中state代表当前鼠标的状态是按下还是抬起

• button为按下的是左、中、右三键中的哪一个

• [x, y]为当前鼠标指针的坐标。次坐标不是世界坐标系，使用时得进行转换，看后面

坐标转换

拿一张图简单说明一下。由于鼠标获取的是世界坐标系下的位置，而在屏幕上绘制点与线是使用的是当前绘图坐标系，所以要进行简单的坐标变换。

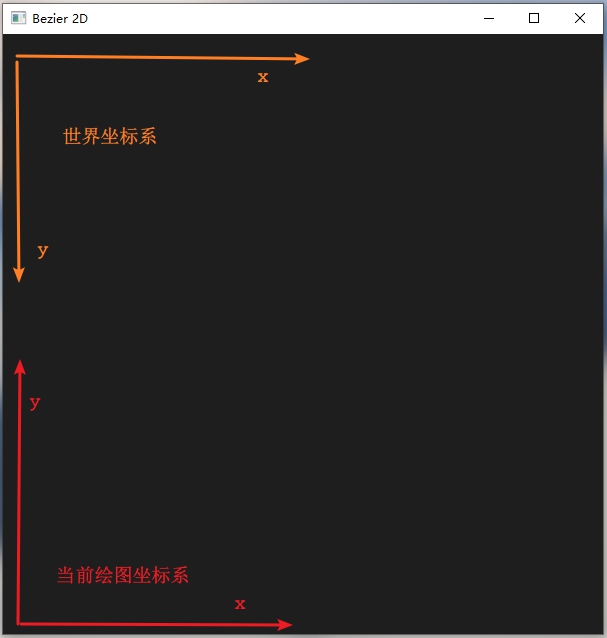
可在显示回调函数中使用如下代码重设OpenGL窗口。

	glViewport(0, 0, (GLsizei)width, (GLsizei)height);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0, width, height, 0);

好了，设置一下前景色和点的大小形状等，来看看画点的效果。

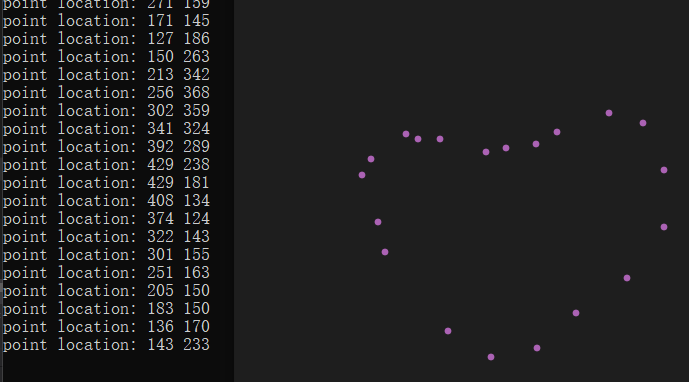
3阶以内的Bezier曲线

对于3阶以内的Bezier曲线，直接将Bezier曲线的定义公式展开，求解系数即可。

void drawBezier_1(vector<int> x, vector<int> y, int num_of_points)
{
	float ax, bx;
	float ay, by;
	int temp_loc = x.size() - 2;

	glColor3f(0.0f, 0.0f, 1.0f);
	drawPixel(x[temp_loc + 0], y[temp_loc + 0], 7);
	drawPixel(x[temp_loc + 1], y[temp_loc + 1], 7);
	ax = x[temp_loc + 0];
	ay = y[temp_loc + 0];
	bx = x[temp_loc + 1];
	by = y[temp_loc + 1];

	float t;
	t = 0.0;
	float dt = 0.002;
	while (t <= 1)
	{
		float x_temp = (1 - t) * ax + t * bx;
		float y_temp = (1 - t) * ay + t * by;
		drawPixel(x_temp, y_temp, 1);
		t += dt;
	}
}

void drawBezier_2(vector<int> x, vector<int> y, int num_of_points)
{
	float ax, bx;
	float ay, by;
	float tSquared;
	int temp_loc = x.size() - 3;

	ax = x[temp_loc + 0] - 2 * x[temp_loc + 1] + x[temp_loc + 2];
	ay = y[temp_loc + 0] - 2 * y[temp_loc + 1] + y[temp_loc + 2];
	bx = x[temp_loc + 0] * (-2) + x[temp_loc + 1] * 2;
	by = y[temp_loc + 0] * (-2) + y[temp_loc + 1] * 2;

	glColor3f(0.0f, 0.0f, 1.0f);
	drawPixel(x[temp_loc + 0], y[temp_loc + 0], 7);
	drawPixel(x[temp_loc + 1], y[temp_loc + 1], 7);
	drawPixel(x[temp_loc + 2], y[temp_loc + 2], 7);

	float t;
	t = 0.0;
	float dt = 0.002;
	while (t <= 1)
	{
		tSquared = t * t;
		float x_temp = ax * tSquared + bx * t + x[temp_loc + 0];
		float y_temp = ay * tSquared + by * t + y[temp_loc + 0];
		drawPixel(x_temp, y_temp, 1);
		t += dt;
	}
}

void drawBezier_3(vector<int> x, vector<int> y, int num_of_points)
{
	float ax, bx, cx;
	float ay, by, cy;
	float tSquared, tCubed;
	int temp_loc = x.size() - 4;

	cx = 3.0 * (x[temp_loc + 1] - x[temp_loc + 0]);
	bx = 3.0 * (x[temp_loc + 2] - x[temp_loc + 1]) - cx;
	ax = x[temp_loc + 3] - x[temp_loc + 0] - cx - bx;

	cy = 3.0 * (y[temp_loc + 1] - y[temp_loc + 0]);
	by = 3.0 * (y[temp_loc + 2] - y[temp_loc + 1]) - cy;
	ay = y[temp_loc + 3] - y[temp_loc + 0] - cy - by;

	glColor3f(0.0f, 0.0f, 1.0f);
	drawPixel(x[temp_loc + 0], y[temp_loc + 0], 7);
	drawPixel(x[temp_loc + 1], y[temp_loc + 1], 7);
	drawPixel(x[temp_loc + 2], y[temp_loc + 2], 7);
	drawPixel(x[temp_loc + 3], y[temp_loc + 3], 7);

	float t;
	t = 0.0;
	float dt = 0.002;
	while (t <= 1)
	{
		tSquared = t * t;
		tCubed = tSquared * t;
		float x_temp = (ax * tCubed) + (bx * tSquared) + (cx * t) + x[temp_loc + 0];
		float y_temp = (ay * tCubed) + (by * tSquared) + (cy * t) + y[temp_loc + 0];
		drawPixel(x_temp, y_temp, 1);
		t += dt;
	}
}

• 对应阶数的函数都可实现，每过阶数+1个点画一次曲线。

n阶Bezier曲线

由Bezier的定义公式我们可以发现，画Bezier曲线需要求组合数 ，求组合数需要求阶乘，然后还需要求幂。因为c++中有求幂的函数,所以实现阶乘和组合数即可。

• 阶乘

  double fac(int n)
  {
  	double result = 1;
  	if (n == 0)
  		return result;
  	for (int i = 1; i <= n; i++){
  		result *= i;
  	}
  	return result;
  }
  

  为了扩大计算范围，使用了double类型

• 组合数

  double combinate(int n, int k)
  {
  	if (k == 0)
  		return 1;
  	double result = 0;
  	result = fac(n) / (fac(k)*(fac(n - k)));
  	return result;
  }
  

  为了扩大计算范围，也使用了double类型，其中k <= n

• n阶Bezier曲线

  void drawBezier(vector<int> x, vector<int> y, int num_of_points) {
  
  	float px = 0.0, py = 0.0; //point current should draw
  	int n;        //number of points -1
  	float t = 0.0, dt = 0.0005; //t in [0, 1], dt is changes each time in t
  	n = x.size() - 1;
  	while (t <= 1) {
  		for (int i = 0; i <= n; i++) {
  			double temp = combinate(n, i)*powf(t, i)*powf(1 - t, n - i);
  			px += temp * x[i];
  			py += temp * y[i];
  		}
  		drawPixel(px, py, 1);
  		t += dt;
  		px = 0.0;
  		py = 0.0;
  	}
  }
  

效果

• 1阶

  

• 2阶

  

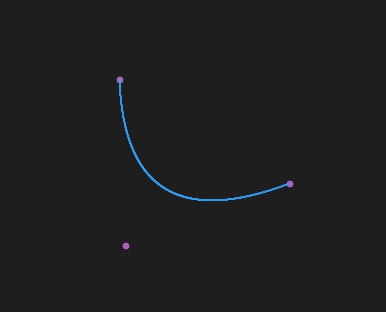
• 3阶

  

• n阶曲线画的❤

  

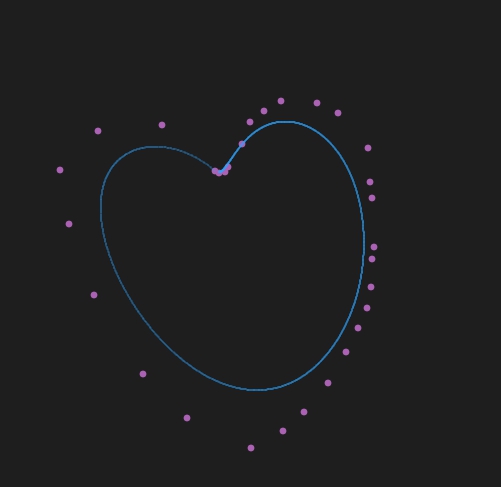
简单而粗暴。。。