ACM 求全排列（字典序、邻位对换、递增进位制数，递减进位制数）

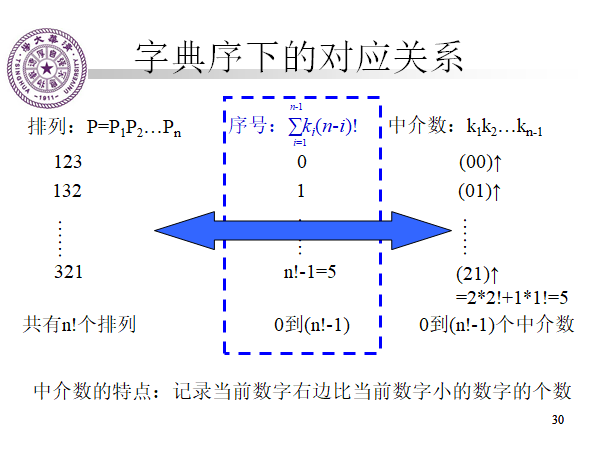
字典序：（联合康托展开就也可以按照中介数求）

邻位对换、递增进位制数，递减进位制数:具体的实现和算法讲解如下：

代码。。C++版的实现并不好。。因为是挨个向后找的，如果K很大的时候会超时，不过。。。思路是这样。。。，第二版C++没有完成。。。因为不想写了，思路很简单，一次加减K就可以了

python代码直接给出，很完美

 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<algorithm>

 using namespace std;
 void Swap(int &a, int &b)
 {
     a == b ?  : a ^= b ^= a ^= b;
 }
 void Print(int A[],int n)
 {
     for (int i = ; i < n; i++)
     {
         printf("%d%c", A[i], i == n -  ? '\n' : ' ');
     }
 }
 //阶乘
 int factorial(int x) { return x >  ? x*factorial(x - ) : ; }
 //字典序法
 void Reverse(int A[],int a,int b)//反转
 {
     while (a < b)
     {
         Swap(A[a], A[b]);
         a++;
         b--;
     }
 }
 bool my_next_permutation(int A[], int n)
 {
     int i = n - ;
     while ((A[i + ] <= A[i])&&i>=)i--;
     if (i<)
     {
         Reverse(A,,n-);
         return false;
     }
     else
     {
         int j = i+;
         while ((A[j] > A[i])&&j<n)j++;
         Swap(A[j-], A[i]);
         Reverse(A ,i+ , n-);
         return true;
     }
 }
 bool my_prev_permutation(int A[], int n)
 {
     int i = n - ;
     while ((A[i + ] >= A[i])&&i>=)i--;
     if (i<)
     {
         Reverse(A,,n-);
         return false;
     }
     else
     {
         int j = i+;
         while ((A[j] < A[i])&&j<n)j++;
         Swap(A[j-], A[i]);
         Reverse(A ,i+ , n-);
         return true;
     }
 }
 //中介数 递增
 int* get_permutation_medium_plus(int A[], int n)//求递增进位制数
 {
     int* temp = new int[n];
     for (int i = ; i < n; i++)
     {
         temp[n-A[i]] = ;
         for (int j = i + ; j <= n - ; j++)
         {
             if (A[j] < A[i])
             {
                 temp[n-A[i]]++;
             }
         }
     }
     return temp;
 }
 int* get_permutation_plus(int medium[], int n)
 {
     int* temp = new int[n];
     memset(temp, , n * sizeof(int));
     for (int i = ; i < n; i++)
     {
         int empty = -,j=n;//防止末尾已经被占的情况故提前一位
         while (empty < medium[i] && j >= )
         {
             j--;
             if (temp[j] <= )
             {
                 empty++;
             }
         }
         temp[j] = n - i;
     }
     return temp;
 }
 void next_permutation_increas_medium_plus(int A[],int n)
 {
     int* mid = get_permutation_medium_plus(A,n);
     int last_ = n-;
     while(){
         if(mid[last_]+<n-last_){
             mid[last_]++;
             break;
         }
         mid[last_] = ;
         last_--;
     }
     int* anstm = get_permutation_plus(mid, n);
     //Print(anstm,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     return;
 }
 void prev_permutation_increas_medium_plus(int A[],int n)
 {
     int* mid = get_permutation_medium_plus(A,n);
     int last_ = n-;
     while(){
         if(mid[last_]->=){
             mid[last_]--;
             break;
         }
         mid[last_] = n-last_-;
         last_--;
     }
     int* anstm = get_permutation_plus(mid, n);
     //Print(anstm,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     //Print(get_permutation_plus(mid, n),n);
     return;
 }
 //递减
 int* get_permutation_medium_sub(int A[], int n)//求递减进位制数
 {
     int* temp = new int[n];
     for (int i = ; i < n; i++)
     {
         temp[n-A[i]] = ;
         for (int j = i + ; j <= n - ; j++)
         {
             if (A[j] < A[i])
             {
                 temp[n-A[i]]++;
             }
         }
     }
     Reverse(temp,,n-);
     return temp;
 }
 int* get_permutation_sub(int medium[], int n)
 {
     int* temp = new int[n];
     memset(temp, , n * sizeof(int));
     for (int i = ; i < n; i++)
     {
         int empty = -, j=n;//防止末尾已经被占的情况故提前一位
         while (empty < medium[n-i-] && j >= )
         {
             j--;
             if (temp[j] <= )
             {
                 empty++;
             }
         }
         temp[j] = n - i;
     }
     return temp;
 }
 void next_permutation_increas_medium_sub(int A[],int n)
 {
     int* mid = get_permutation_medium_sub(A,n);
     //Print(mid,n);
     int last_ = ;
     while(){
         if(mid[n-last_]+<n-last_+){
             mid[n-last_]++;
             break;
         }
         mid[n-last_] = ;
         last_++;
     }
     int* anstm = get_permutation_sub(mid, n);
     //Print(mid,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     return;
 }
 void prev_permutation_increas_medium_sub(int A[],int n)
 {
     int* mid = get_permutation_medium_sub(A,n);
     //Print(mid,n);
     int last_ = ;
     while(){
         if(mid[n-last_]->=){
             mid[n-last_]--;
             break;
         }
         mid[n-last_] = n-last_;
         last_++;
     }
     int* anstm = get_permutation_sub(mid, n);
     //Print(anstm,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     //Print(get_permutation_plus(mid, n),n);
     return;
 }
 //邻位对换法
 int my_find(int A[],int n, int key){
     for(int i = ; i < n; i++){
         if(A[i]==key) return i;
     }
     return -;
 }
 int* get_permutation_medium_neighbor(int A[], int dirct[], int n)//求递减进位制数
 {
     //dirct[]标记方向,-1向左 1向右
     int* temp = new int[n];
     temp[] = ;
     dirct[] = ;
     for(int i = ; i <= n; i++){
         int id_ = my_find(A,n,i);
         if(i==) dirct[i-] = -;
         else if(i%==){
             if(temp[i-]%==)dirct[i-] = ;
             else dirct[i-]=-;
         }
         else if(i%==){
             if((temp[i-]+temp[i-])%==) dirct[i-] = ;
             else dirct[i-]=-;
         }
         int j = id_;
         int bi_ = ;
         while(j < n && j>=){
             if(A[j]<i) bi_++;
             j += -dirct[i-]*;
         }
         temp[i-] = bi_;
     }
     return temp;
 }
 int* get_permutation_neighbor(int medium[], int dirct[] ,int n)
 {
     int* temp = new int[n];
     for(int i = ; i < n; i++) temp[i] = ;
     for (int i = ; i < n; i++)
     {
         if((n-i+)==) dirct[n-i]=-;
         else if((n-i+)%==){
             if(medium[n-i-]%==) dirct[n-i]=;
             else dirct[n-i]=-;
         }
         else if((n-i+)%==){
             if((medium[n-i-] + medium[n-i-])%==) dirct[n-i] = ;
             else dirct[n-i] = -;
         }
         if(dirct[n-i] == -){
             int j = n-;int empty = ;
             while(empty <= medium[n-i]&&j>=){
                 if(temp[j]==) empty++;
                 j--;
             }
             temp[j+] = n-i+;
         }
         else{
             int j = ;int empty = ;
             while(empty <= medium[n-i]&&j<n){
                 if(temp[j]==) empty++;
                 j++;
             }
             temp[j-] = n-i+;
         }
         //Print(temp,n);
     }
     //Print(medium,n);
     //Print(dirct,n);
     return temp;
 }
 void next_permutation_increas_medium_neighbor(int A[],int dirct[],int n)
 {
     int* mid = get_permutation_medium_neighbor(A,dirct,n);
     //Print(mid,n);
     //Print(dirct,n);
     int last_ = ;
     while(){
         if(mid[n-last_]+<n-last_+){
             mid[n-last_]++;
             break;
         }
         mid[n-last_] = ;
         last_++;
     }
     int* anstm = get_permutation_neighbor(mid,dirct, n);
     //Print(mid,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     return;
 }
 void prev_permutation_increas_medium_neighbor(int A[],int dirct[],int n)
 {
     int* mid = get_permutation_medium_neighbor(A,dirct,n);
     //Print(mid,n);
     int last_ = ;
     while(){
         if(mid[n-last_]->=){
             mid[n-last_]--;
             break;
         }
         mid[n-last_] = n-last_;
         last_++;
     }
     int* anstm = get_permutation_neighbor(mid, dirct,n);
     //Print(anstm,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     //Print(get_permutation_plus(mid, n),n);
     return;
 }

 int main()
 {
     int n,type,k;
     while(~scanf("%d%d%d",&n,&type,&k)){
         int tm[n];
         for(int i = ; i < n; i++){
             scanf("%d",&tm[i]);
         }
         if(type==){
             if(k>=){
                 while(k--) next_permutation(tm,tm+n);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 while(k--) prev_permutation(tm,tm+n);
                 Print(tm,n);
             }
             /*下面自己写的实现竟然超时了，气人
             if(k>=0){
                 while(k--) my_next_permutation(tm,n);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 while(k--) my_prev_permutation(tm,n);
                 Print(tm,n);
             }
             */
         }
         else if(type==){
             if(k>=){
                 while(k--) next_permutation_increas_medium_plus(tm,n);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 while(k--) prev_permutation_increas_medium_plus(tm,n);
                 Print(tm,n);
             }
         }
         else if(type==){
             if(k>=){
                 while(k--) next_permutation_increas_medium_sub(tm,n);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 while(k--) prev_permutation_increas_medium_sub(tm,n);
                 Print(tm,n);
             }
         }
         else{
             int dict[n];
             if(k>=){
                 while(k--) next_permutation_increas_medium_neighbor(tm,dict,n);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 while(k--) prev_permutation_increas_medium_neighbor(tm,dict,n);
                 Print(tm,n);
             }
         }
     }
     return ;
 }

 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<algorithm>
 #include<cmath>

 using namespace std;
 void Swap(int &a, int &b)
 {
     a == b ?  : a ^= b ^= a ^= b;
 }
 void Print(int A[],int n)
 {
     for (int i = ; i < n; i++)
     {
         printf("%d%c", A[i], i == n -  ? '\n' : ' ');
     }
 }
 //阶乘
 int factorial(int x) { return x >  ? x*factorial(x - ) : ; }
 //字典序法
 void Reverse(int A[],int a,int b)//反转
 {
     while (a < b)
     {
         Swap(A[a], A[b]);
         a++;
         b--;
     }
 }
 bool my_next_permutation(int A[], int n)
 {
     int i = n - ;
     while ((A[i + ] <= A[i])&&i>=)i--;
     if (i<)
     {
         Reverse(A,,n-);
         return false;
     }
     else
     {
         int j = i+;
         while ((A[j] > A[i])&&j<n)j++;
         Swap(A[j-], A[i]);
         Reverse(A ,i+ , n-);
         return true;
     }
 }
 bool my_prev_permutation(int A[], int n)
 {
     int i = n - ;
     while ((A[i + ] >= A[i])&&i>=)i--;
     if (i<)
     {
         Reverse(A,,n-);
         return false;
     }
     else
     {
         int j = i+;
         while ((A[j] < A[i])&&j<n)j++;
         Swap(A[j-], A[i]);
         Reverse(A ,i+ , n-);
         return true;
     }
 }
 //用中介数求字典序法

 //中介数 递增
 int* get_permutation_medium_plus(int A[], int n)//求递增进位制数
 {
     int* temp = new int[n];
     for (int i = ; i < n; i++)
     {
         temp[n-A[i]] = ;
         for (int j = i + ; j <= n - ; j++)
         {
             if (A[j] < A[i])
             {
                 temp[n-A[i]]++;
             }
         }
     }
     return temp;
 }
 int* get_permutation_plus(int medium[], int n)
 {
     int* temp = new int[n];
     memset(temp, , n * sizeof(int));
     for (int i = ; i < n; i++)
     {
         int empty = -,j=n;//防止末尾已经被占的情况故提前一位
         while (empty < medium[i] && j >= )
         {
             j--;
             if (temp[j] <= )
             {
                 empty++;
             }
         }
         temp[j] = n - i;
     }
     return temp;
 }
 void next_permutation_increas_medium_plus(int A[],int n,int k)
 {
     int* mid = get_permutation_medium_plus(A,n);
     int last_ = n-;
     while(){
         if(mid[last_]+k<n-last_){
             mid[last_] += k;
             break;
         }
         int dim = (mid[last_]+k);
         mid[last_] = (mid[last_]+k)%(n-last_);
         k = dim/(n-last_);
         last_--;
     }
     int* anstm = get_permutation_plus(mid, n);
     //Print(anstm,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     return;
 }

 void prev_permutation_increas_medium_plus(int A[],int n,int k)
 {
     int* mid = get_permutation_medium_plus(A,n);
     int last_ = n-;
     while(){
         if(mid[last_]-k>=){
             mid[last_]-=k;
             break;
         }
         int dim = (k-mid[last_]);
         int c = ceil(double(dim)/(n-last_));
         mid[last_] = c*(n-last_)-(k-mid[last_]);
         k = c;
         last_--;
     }
     int* anstm = get_permutation_plus(mid, n);
     //Print(anstm,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     //Print(get_permutation_plus(mid, n),n);
     return;
 }

 //递减
 int* get_permutation_medium_sub(int A[], int n)//求递减进位制数
 {
     int* temp = new int[n];
     for (int i = ; i < n; i++)
     {
         temp[n-A[i]] = ;
         for (int j = i + ; j <= n - ; j++)
         {
             if (A[j] < A[i])
             {
                 temp[n-A[i]]++;
             }
         }
     }
     Reverse(temp,,n-);
     return temp;
 }
 int* get_permutation_sub(int medium[], int n)
 {
     int* temp = new int[n];
     memset(temp, , n * sizeof(int));
     for (int i = ; i < n; i++)
     {
         int empty = -, j=n;//防止末尾已经被占的情况故提前一位
         while (empty < medium[n-i-] && j >= )
         {
             j--;
             if (temp[j] <= )
             {
                 empty++;
             }
         }
         temp[j] = n - i;
     }
     return temp;
 }
 void next_permutation_increas_medium_sub(int A[],int n,int k)
 {
     int* mid = get_permutation_medium_sub(A,n);
     //Print(mid,n);
     int last_ = ;
     while(){
         if(mid[n-last_]+k<n-last_+){
             mid[n-last_] += k;
             break;
         }
         int dim = (mid[n-last_]+k);
         mid[n-last_] = (mid[n-last_]+k)%(n-last_+);
         k = dim/(n-last_+);
         last_++;
     }
     int* anstm = get_permutation_sub(mid, n);
     //Print(mid,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     return;
 }
 void prev_permutation_increas_medium_sub(int A[],int n,int k)
 {
     int* mid = get_permutation_medium_sub(A,n);
     //Print(mid,n);
     int last_ = ;
     while(){
         if(mid[n-last_]-k>=){
             mid[n-last_]-=k;
             break;
         }
         int dim = (k-mid[n-last_]);
         int c = ceil(double(dim)/(n-last_+));
         mid[n-last_] = c*(n-last_+)-(k-mid[n-last_]);
         k = c;
         last_++;
     }
     int* anstm = get_permutation_sub(mid, n);
     //Print(anstm,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     //Print(get_permutation_plus(mid, n),n);
     return;
 }
 //邻位对换法
 int my_find(int A[],int n, int key){
     for(int i = ; i < n; i++){
         if(A[i]==key) return i;
     }
     return -;
 }
 int* get_permutation_medium_neighbor(int A[], int dirct[], int n)//求递减进位制数
 {
     //dirct[]标记方向,-1向左 1向右
     int* temp = new int[n];
     temp[] = ;
     dirct[] = ;
     for(int i = ; i <= n; i++){
         int id_ = my_find(A,n,i);
         if(i==) dirct[i-] = -;
         else if(i%==){
             if(temp[i-]%==)dirct[i-] = ;
             else dirct[i-]=-;
         }
         else if(i%==){
             if((temp[i-]+temp[i-])%==) dirct[i-] = ;
             else dirct[i-]=-;
         }
         int j = id_;
         int bi_ = ;
         while(j < n && j>=){
             if(A[j]<i) bi_++;
             j += -dirct[i-]*;
         }
         temp[i-] = bi_;
     }
     return temp;
 }
 int* get_permutation_neighbor(int medium[], int dirct[] ,int n)
 {
     int* temp = new int[n];
     for(int i = ; i < n; i++) temp[i] = ;
     for (int i = ; i < n; i++)
     {
         if((n-i+)==) dirct[n-i]=-;
         else if((n-i+)%==){
             if(medium[n-i-]%==) dirct[n-i]=;
             else dirct[n-i]=-;
         }
         else if((n-i+)%==){
             if((medium[n-i-] + medium[n-i-])%==) dirct[n-i] = ;
             else dirct[n-i] = -;
         }
         if(dirct[n-i] == -){
             int j = n-;int empty = ;
             while(empty <= medium[n-i]&&j>=){
                 if(temp[j]==) empty++;
                 j--;
             }
             temp[j+] = n-i+;
         }
         else{
             int j = ;int empty = ;
             while(empty <= medium[n-i]&&j<n){
                 if(temp[j]==) empty++;
                 j++;
             }
             temp[j-] = n-i+;
         }
         //Print(temp,n);
     }
     //Print(medium,n);
     //Print(dirct,n);
     return temp;
 }
 void next_permutation_increas_medium_neighbor(int A[],int dirct[],int n,int k)
 {
     int* mid = get_permutation_medium_neighbor(A,dirct,n);
     //Print(mid,n);
     //Print(dirct,n);
     int last_ = ;
     while(){
         if(mid[n-last_]+k<n-last_+){
             mid[n-last_] += k;
             break;
         }
         int dim = (mid[n-last_]+k);
         mid[n-last_] = (mid[n-last_]+k)%(n-last_+);
         k = dim/(n-last_+);
         last_++;
     }
     int* anstm = get_permutation_neighbor(mid,dirct, n);
     //Print(mid,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     return;
 }
 void prev_permutation_increas_medium_neighbor(int A[],int dirct[],int n,int k)
 {
     int* mid = get_permutation_medium_neighbor(A,dirct,n);
     //Print(mid,n);
     int last_ = ;
     while(){
         if(mid[n-last_]-k>=){
             mid[n-last_]-=k;
             break;
         }
         int dim = (k-mid[n-last_]);
         int c = ceil(double(dim)/(n-last_+));
         mid[n-last_] = c*(n-last_+)-(k-mid[n-last_]);
         k = c;
         last_++;
     }
     int* anstm = get_permutation_neighbor(mid, dirct,n);
     //Print(anstm,n);
     for(int i = ; i < n; i++) A[i] = anstm[i];
     //Print(get_permutation_plus(mid, n),n);
     return;
 }

 int main()
 {
     int n,type,k;
     while(~scanf("%d%d%d",&n,&type,&k)){
         int tm[n];
         for(int i = ; i < n; i++){
             scanf("%d",&tm[i]);
         }

         if(type==){
            /* if(k>=0){
                 my_next_permutation(tm,n,k);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 my_prev_permutation(tm,n,k);
                 Print(tm,n);
             }
             下面自己写的实现竟然超时了，气人
             if(k>=0){
                 while(k--) my_next_permutation(tm,n);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 while(k--) my_prev_permutation(tm,n);
                 Print(tm,n);
             }*/

         }

         else if(type==){
             if(k>=){
                 next_permutation_increas_medium_plus(tm,n,k);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 prev_permutation_increas_medium_plus(tm,n,k);
                 Print(tm,n);
             }

         }
         else if(type==){
             if(k>=){
                 next_permutation_increas_medium_sub(tm,n,k);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 prev_permutation_increas_medium_sub(tm,n,k);
                 Print(tm,n);
             }
         }
         else{
             int dict[n];
             if(k>=){
                 next_permutation_increas_medium_neighbor(tm,dict,n,k);
                 Print(tm,n);
             }
             else{
                 k = -k;
                 prev_permutation_increas_medium_neighbor(tm,dict,n,k);
                 Print(tm,n);
             }
         }
     }
     return ;
 }

C++ 修改版

 #!/usr/bin/env python
 # coding: utf-8

 # In[2]:

 def dictionary(a,b):
     zhongjie=[]
     for i in range(len(b)-1):
         sum0=0
         for j in b[(i+1):]:
             if j<b[i]:
                 sum0+=1
         zhongjie.append(sum0)
     xushu=zhongjie_to_ten(zhongjie)+a[2]
     zhongjie=ten_to_zhongjie(a[0],xushu)
     result=zhongjie_to_pailie(zhongjie)
     return result

 # In[3]:

 def increase(a,b):
     temp=inc_paixu_zhongjie(b)
     temp=zhongjie_to_ten(temp)+a[2]
     temp=ten_to_zhongjie(a[0],temp)
     result=inc_zhongjie_paixu(temp)
     result.reverse()
     return result

 # In[4]:

 def decrease(a,b):
     zhongjie=inc_paixu_zhongjie(b)
     zhongjie.reverse()
     xuhao=int(dec_zhongjie_ten(zhongjie))
     xuhao+=int(a[2])
     zhongjie=dec_ten_zhongjie(a[0],xuhao)
     zhongjie.reverse()
     result=inc_zhongjie_paixu(zhongjie)
     result.reverse()
     return result

 # In[30]:

 def exchange(a,b):
     zhongjie=exc_paixu_zhongjie(b)
     xuhao=int(dec_zhongjie_ten(zhongjie))
     xuhao1=int(a[2])+xuhao
     zhongjie=dec_ten_zhongjie(a[0],xuhao1)
     result=exc_zhongjie_paixu(zhongjie)
     return result

 # In[6]:

 ##exchange
 def exc_paixu_zhongjie(b):
     direction=[0]*len(b)
     zhongjie=[0]*(len(b)-1)
     ##向左为0，向右为1
     sum0=0
     for i in b[(b.index(2)):]:
         if i<2:
             sum0+=1
     zhongjie[0]=sum0
     for i in range(3,len(b),2):
         ##奇数位
         direction[b.index(i)]=zhongjie[i-3]%2
         if direction[b.index(i)]:
             sum0=0
             for j in b[0:(b.index(i))]:
                 if j<i:
                     sum0+=1
             zhongjie[i-2]=sum0
         else:
             sum0=0
             for j in b[(b.index(i)):]:
                 if j<i:
                     sum0+=1
             zhongjie[i-2]=sum0
         ##偶数位
         direction[b.index(i+1)]=(zhongjie[i-3]+zhongjie[i-2])%2
         if direction[b.index(i+1)]:
             sum0=0
             for j in b[0:(b.index(i+1))]:
                 if j<(i+1):
                     sum0+=1
             zhongjie[i-1]=sum0
         else:
             sum0=0
             for j in b[(b.index(i+1)):]:
                 if j<(i+1):
                     sum0+=1
             zhongjie[i-1]=sum0
     if len(b)%2==1:
         direction[b.index(len(b))]=zhongjie[len(b)-3]%2
         if direction[b.index(len(b))]:
             sum0=0
             for j in b[0:(b.index(len(b)))]:
                 if j<len(b):
                     sum0+=1
             zhongjie[len(b)-2]=sum0
         else:
             sum0=0
             for j in b[(b.index(len(b))):]:
                 if j<len(b):
                     sum0+=1
             zhongjie[len(b)-2]=sum0
     return zhongjie

 def exc_zhongjie_paixu(zhongjie):
     paixu=[1]*(len(zhongjie)+1)
     for i in range(len(paixu),2,-1):
         if i%2==1:##奇数
             if zhongjie[i-3]%2==1:##向右

                 sum0=0
                 for j in range(len(paixu)):
                     sum0+=(paixu[j]==1)
                     if sum0==zhongjie[i-2]+1:
                         paixu[j]=i
                         break
             else:#向左
                 paixu.reverse()
                 sum0=0
                 for j in range(len(paixu)):
                     sum0+=(paixu[j]==1)
                     if sum0==zhongjie[i-2]+1:
                         paixu[j]=i
                         paixu.reverse()
                         break 

         else:#偶数
             if (zhongjie[i-4]+zhongjie[i-3])%2==1:##向右
                 sum0=0
                 for j in range(len(paixu)):
                     sum0+=(paixu[j]==1)
                     if sum0==zhongjie[i-2]+1:
                         paixu[j]=i
                         break
             else:#向左
                 paixu.reverse()
                 sum0=0
                 for j in range(len(paixu)):
                     sum0+=(paixu[j]==1)
                     if sum0==zhongjie[i-2]+1:
                         paixu[j]=i
                         paixu.reverse()
                         break
     if zhongjie[0]==0:
         paixu.reverse()
     paixu[paixu.index(1)]=2
     if zhongjie[0]==0:
         paixu.reverse()
     return paixu

 # In[58]:

 ###decrease###
 def dec_zhongjie_ten(zhongjie):
     sum0=0
     for i in range(len(zhongjie)):
         sum0+=zhongjie[i]*int(jiecheng(len(zhongjie)+1))//int(jiecheng(i+2))
     return sum0
 def idec_zhongjie_ten(zhongjie):
     sum0=zhongjie[0]
     for i in range(3,len(zhongjie)+2):
         sum0=sum0*i+zhongjie[i-2]
     return sum0
 def dec_ten_zhongjie(n,xuhao):
     abs_n=int(xuhao)
     out=[0]*(n-1)
     for i in range(n,1,-1):
         out[i-2]=abs_n%i
         abs_n=abs_n//i
     return out

 # In[8]:

 ###increase###
 def inc_paixu_zhongjie(b):##增序排序到中介数
     result=[]
     for i in range(len(b),1,-1):
         sum0=0
         for j in b[(b.index(i)):]:
             if j<i:
                 sum0+=1
         result.append(sum0)
     return result
 def error(zhongjie):
     paixu=[1]*(len(zhongjie)+1)##逆序数，最后倒置
     for i in range(len(zhongjie)):
         sum=0
         for j in range(len(paixu)):
             if paixu[j]==1:
                 sum+=1
             if sum==zhongjie[i] and paixu[j+1]==1:
                 paixu[j+1]=len(zhongjie)+1-i
                 break
             if zhongjie[i]==0 and paixu[j]==1:
                 paixu[j]=len(zhongjie)+1-i
                 break
     paixu.reverse()
     return  paixu
 def inc_zhongjie_paixu(zhongjie):
     paixu=[1]*(len(zhongjie)+1)
     for i in range(len(zhongjie)):
         sum0=0
         for j in range(len(paixu)):
             if paixu[j]==1:
                 if sum0==zhongjie[i]:
                     paixu[j]=len(paixu)-i
                     break
                 else:
                     sum0+=1
     paixu.reverse
     return paixu

 # In[32]:

 #######字典序#######
 def jiecheng(n):##阶乘
     if n==0 or n==1 or n>20:
         return 1
     else:
         return int(n*jiecheng(n-1))
 def ten_to_zhongjie(n,ten):##十进制转换中介数
     abs_n=abs(ten)
     out=[]
     for i in range(n-1,0,-1):
         zheng=abs_n//jiecheng(i)
         abs_n=abs_n%jiecheng(i)
         out.append(zheng)
     return out
 def zhongjie_to_ten(zhongjie):##中介数转换10进制
     sum=0
     for  i in range(len(zhongjie)):
         sum=sum+zhongjie[-(i+1)]*jiecheng(i+1)
     return sum
 def zhongjie_to_pailie(zhongjie):##中介数转排列
     pailie=[]
     for i in range(len(zhongjie)):
         temp=sorted(pailie)
         pailie_new=zhongjie[i]+1
         for j in temp:
             if j<=pailie_new:
                 pailie_new=pailie_new+1
         pailie.append(pailie_new)
     for i in range(len(pailie)+1):
         if (i+1) not in pailie:
             pailie.append(i+1)
     return pailie

 # In[33]:

 #a=input()
 #b=input()
 ##初始化
 #a=a.split()
 #b=b.split()
 #for i in range(len(a)):
  #   a[i]=int(a[i])
 #for i in range(a[0]):
   #  b[i]=int(b[i])
 a=list(map(int,input().split(" ")[:3]))
 b=list(map(int,input().split(" ")[:a[0]]))
     ##分类运算
 if a[1]==1:
     output=dictionary(a,b)
 elif a[1]==2:
     output=increase(a,b)
 elif a[1]==3:
     output=decrease(a,b)
 elif a[1]==4:
     output=exchange(a,b)
 else :
     output=b

 #输出
 for i in range(a[0]):
     output[i]=str(output[i])
 print(" ".join(output))

 # In[ ]: