paper 142：SDM算法--Supervised Descent Method

对于face recognition的研究，我是认真的（认真expression，哈哈哈~~~~~~）许久没有写blog了，欢迎一起讨论。

SDM(Supvised Descent Method)方法主要是应用在人脸对齐上。SDM本是一种求函数逼近的方法，可以用于最小二乘求解。SDM并非一种人脸对齐方法，只是作者在提出新的人脸对齐方法中运用了自己的最小二乘方法。文章：Supervised Descent Method and its Applications to Face Alignment。这篇文章提出了一种基于机器学习来解决复杂最小二乘问题(least squares problem)的方法  (简称SDM方法)。，从训练数据中学习梯度下降的方向并建立相应的回归模型，然后利用得到的模型来进行梯度方向估计。

什么是人脸对齐？其实就是人脸特征点定位，需要先人工指定点的具有规律的位置，然后在输入的人脸上按照特征点分布规律把点标记出来。

 1、 Motivation（问题的由来）

最小二乘问题中，用牛顿法求解是常用的办法，但用在求解计算机视觉的问题的时候，会遇到一些问题，比如1）、Hessian矩阵最优在局部最优的时候才是正定的，其他地方可能就不是正定的了，这就意味着求解出来的梯度方向未必是下降的方向；2）、牛顿法要求目标函数是二次可微的，但实际中未必就一定能达到要求的了；3）、Hessian矩阵会特别的大，比如人脸对其中有66个特征点，每个特征点有128维度，那么展成的向量就能达到66x128=8448，从而Hessian矩阵就能达到8448x8448，如此大维度的逆矩阵求解，是计算量特别大的（O(p^3)次的操作和O(p^2)的存储空间）。因此避免掉Hessian矩阵的计算，Hessian不正定问题，大存储空间和计算量，寻找这样一种方法是上述论文要解决的问题。

2、解决方式

梯度下降法的关键是找到梯度方向和步长，对于计算机视觉问题，牛顿法求解未必能常常达到好的下降方向和步长，如下图所示：

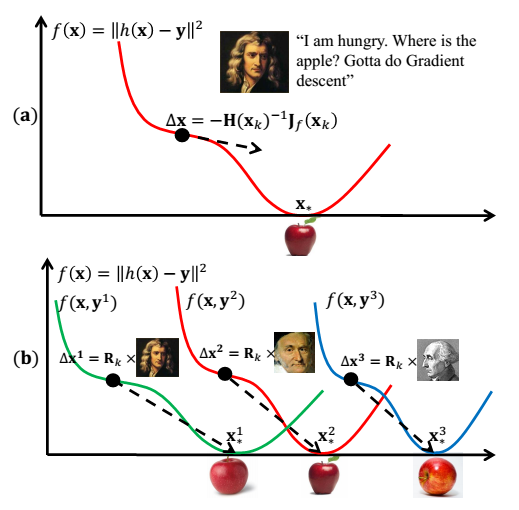
　　（a）为牛顿法的下降量，收敛不能达到最理想的步长和方向。而（b）本文的SDM算法，对于不同的正面侧面等情况都能得到很好的收敛方向和步长。

思考一下，能不能从别的角度来估计Hessian矩阵和梯度向量，或者，Hessian矩阵的逆与梯度向量的乘积呢？(使用牛顿法，梯度向量与Hessian逆矩阵的乘积直接决定了优化方向，所以如果可以直接估计他们的乘积，效果上是一样的。)
       如何实现，尝试使用大量的数据里面构造出这个关键的矩阵/向量。假设要求解的最小二乘问题是 || f(x) - y ||^2 ，其中f是一个非常复杂的函数，它的计算方法已知，但是梯度和Hessian矩阵均无法直接求解。只要给定一个足够大的最优解集合 {(x*, y*) }， 就可以通过模拟牛顿法的过程来逐步构造出Hessian矩阵和梯度向量。不过直接构造Hessian矩阵和梯度向量需要比较多的训练数据，因为自由度往往很大。既然牛顿法里面最后只需要Hessian的逆和梯度向量的乘积(，估计这个向量显然要直接得多，也容易一些。SDM方法假设这个乘积是x的一个复杂函数，并且假设这个函数可以被一组函数的线性组合近似。具体而言，SDM用以下迭代公式

x_{k+1} = x_k + R_k * f(x_k) + b_k

取代了牛顿法的迭代公式

x_{k+1} = x_k - H(x)^{-1} f'(x)

其中R_k 和 b_k 是学习得到的用于近似Hessian矩阵和梯度的模型参数。通过模拟牛顿法的过程，可以通过不断得修正一组初始估计来逼近最优解集合，每一步迭代都可以计算出一对R_k 和 b_k，它们一起构成了最后的模型。
      求解 R_k 和 b_k 的方法类似于贪心算法，即在每一步，最小化迭代后的值与最优值的差:

|| x* - x_k + R_k * f(x_k) + b_k ||^2

这个其实就是最简单的线性最小二乘问题，可以很容易的求解。
      当然啦，实际训练的时候，需要在所有训练样例计算上面的代价函数并求和，得到最终的代价函数，然后再求解R_k和b_k。

3、 实验结果

a、真实结果和拟合结果比较图：

SDM接近于真实的标记结果，拟合结果很好。（红色的为Ground True，绿色的为SDM拟合结果）

b、SDM 和 Netown的迭代收敛比较图：

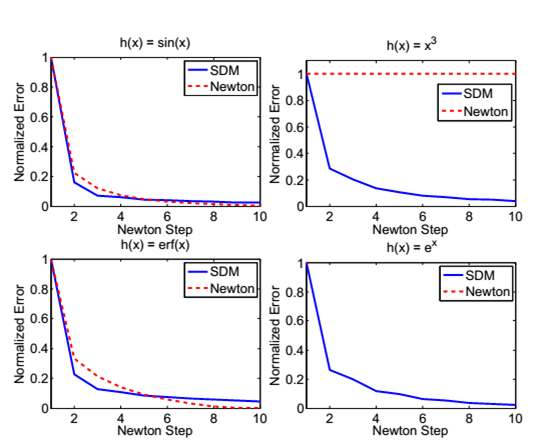
牛顿迭代法出现迭代失败的情况，而SDM均可以迭代至收敛。

c、指定跟踪算法和SDM比较图：

指定跟踪器会出现过拟合的现象，而SDM表现则相当的稳定

参考：http://www.cnblogs.com/cv-pr/p/4797823.html

http://www.thinkface.cn/thread-2913-1-1.html

[1]  Supervised Descent Method and its Applications to Face Alignment

[2]  Cascaded Regressor based 3D Face Reconstruction from a Single Arbitrary View Image

codes：C++  ：https://github.com/RoboPai/sdm

https://github.com/guozhongluo/SDM

MATLAB：https://github.com/tntrung/sdm_face_alignment

https://github.com/fagg/SDM-Face-Alignment