正则化的L1范数和L2范数

范数介绍：https://www.zhihu.com/question/20473040?utm_campaign=rss&utm_medium=rss&utm_source=rss&utm_content=title

首先介绍损失函数，它是用来估量你模型的预测值f(x)与真实值Y的不一致程度

主要的几种类型包括：1）0-1损失函数  2）平方损失函数   3）绝对损失函数  4） 对数损失函数

0-1损失函数：

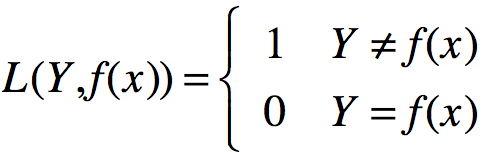
平方损失函数：

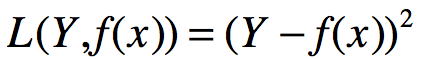
绝对损失函数：

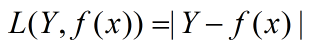
对数损失函数：

由此延伸出对应的概念：

其次介绍一般的范数表示：

范数包括向量范数和矩阵范数，向量范数表征向量空间中向量的大小，矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是，对应向量范数，向量空间中的向量都是有大小的，这个大小如何度量，就是用范数来度量的，不同的范数都可以来度量这个大小

向量的范数：

1-范数，计算方式为向量所有元素的绝对值之和。

2-范数，计算方式跟欧式距离的方式一致。

 

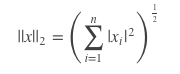
矩阵的范数：

假设矩阵的大小为m∗n，即m行n列。

1-范数，又名列和范数。顾名思义，即矩阵列向量中绝对值之和的最大值。

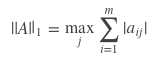
2-范数，又名谱范数，计算方法为ATA矩阵的最大特征值的开平方。

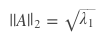
其中λ1为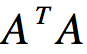的最大特征值。

 

正则化也就是经验风险项加上正则化项，从而达到对模型选择的目的，以做到从模型拟合效果（经验风险）和复杂度（正则化项）来选去最优模型。

正则化的一般表示形式为：

　　　　　　　　  

其中第一项表示经验风险，第二项表示正则化项

正则化可以表示为多个形式，以回归方程为例，由于其损失函数为平方损失，正则化表示为参数向量的L2范数：

　　　　　　　　

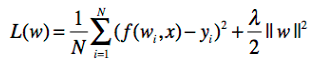
在这里||w||表示参数向量w的L2范数。

正则化也可以表示为参数向量的L1范数

　　　　　　　　

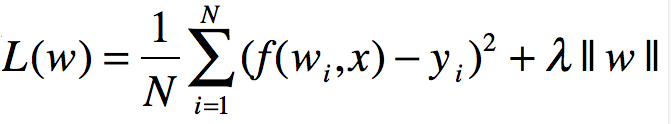
其中||w||表示参数向量w的L1范数

以上部分的经验风险表现越小模型越复杂，这时候正则化项为表现较大，所以我们主要还是筛选经验风险和正则化项同时较小的模型。

注：

L1范数因为表现出比L0范数更好的求解性而应用较为广泛

L2范数表现为向量各元素平方和求平方根，我们让L2范数的正则项||W||2最小，可以使得W的每个元素都很小，都接近于0。