[伯努利数] poj 1707 Sum of powers

题目链接：

http://poj.org/problem?id=1707

Language:
Default

Sum of powers

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 735		Accepted: 354

Description

A young schoolboy would like to calculate the sum 
 
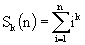for some fixed natural k and different natural n. He observed that calculating i^k for all i (1<=i<=n) and summing up results is a too slow way to do it, because the number of required arithmetical operations increases as n increases. Fortunately,
there is another method which takes only a constant number of operations regardless of n. It is possible to show that the sum S_k(n) is equal to some polynomial of degree k+1 in the variable n with rational coefficients, i.e.,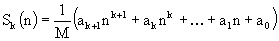 
 
We require that integer M be positive and as small as possible. Under this condition the entire set of such numbers (i.e. M, a_k+1, a_k, ... , a₁, a₀) will be unique for the given k. You have to write a program to find
such set of coefficients to help the schoolboy make his calculations quicker.

Input

The input file contains a single integer k (1<=k<=20).

Output

Write integer numbers M, a_k+1, a_k, ... , a₁, a₀ to the output file in the given order. Numbers should be separated by one space. Remember that you should write the answer with the smallest positive M possible.

Sample Input

2

Sample Output

6 2 3 1 0

Source

Northeastern Europe 1997

题目意思：

已知而且求最小的M。使得a[k+1]---a[0]都为整数。

解题思路：
伯努利数：http://zh.wikipedia.org/wiki/%E4%BC%AF%E5%8A%AA%E5%88%A9%E6%95%B0

所以有1^k+2^k+3^k+...+n^k=1/(k+1)(C[k+1,0)*B[0]*n^(k+1-0)+C[k+1,1]*B[1]*n^(k+1-1)+...+C[k+1,j]*B[j]*n^(k+1-j)+...+C[k+1,k]*B[k]*n^(k+1-k))+n^k

先求出伯努利数，然后分母求最小公倍数就可以。

注意n^k的系数要加上后面的n^k为C[k+1,1]*B[1]+(k+1)

最后仅仅剩下分数加法了。

注意最大公约数为负数的情况，强制转化为正数，用分子保存整个分数的正负性。

代码：

//#include<CSpreadSheet.h>

#include<iostream>
#include<cmath>
#include<cstdio>
#include<sstream>
#include<cstdlib>
#include<string>
#include<string.h>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#include<ctime>
#include<bitset>
#include<cmath>
#define eps 1e-6
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define ll __int64
#define LL long long
#define lson l,m,(rt<<1)
#define rson m+1,r,(rt<<1)|1
#define M 1000000007
//#pragma comment(linker, "/STACK:1024000000,1024000000")
using namespace std;

#define Maxn 25
ll C[Maxn][Maxn];
struct PP
{
    ll a,b;
}B[Maxn],ans[Maxn];

ll k;

ll gcd(ll a,ll b)
{
    if(a%b==0)
    {
        if(b>0)
            return b;
        return -b;
    }

    return gcd(b,a%b);
}

PP add(PP a,PP b) //模拟两个分数的加法
{
    if(!a.a) //假设有一个为0
        return b;
    if(!b.a)
        return a;

    ll temp=a.b/gcd(a.b,b.b)*b.b; //求出分母的最小公倍数
    //printf("%I64d\n",temp);
    PP res;
    res.a=temp/a.b*a.a+temp/b.b*b.a; //分子相加
    res.b=temp;

    if(res.a)  //约掉最大公约数
    {
        ll tt=gcd(res.a,res.b);
        res.b/=tt;
        res.a/=tt;
    }
    return res;

}

void init()
{
    memset(C,0,sizeof(C));

    for(int i=0;i<=25;i++)
    {
        C[i][0]=1;
        for(int j=1;j<i;j++)
            C[i][j]=C[i-1][j]+C[i-1][j-1];
        C[i][i]=1;
    }
    B[0].a=1,B[0].b=1;  //求伯努利数

    for(int i=1;i<=20;i++)  //用递推关系求
    {
        PP temp;
        temp.a=0;
        temp.b=0;

        for(int j=0;j<i;j++)
        {
            PP tt=B[j];

            tt.a=tt.a*C[i+1][j];
            //printf("::::%I64d %I64d:\n",tt.a,tt.b);
            if(tt.a)
            {
                ll te=gcd(tt.a,tt.b);
                tt.a/=te;
                tt.b/=te;
            }

            temp=add(temp,tt);

            //printf("i:%d j:%d %I64d %I64d:\n",i,j,temp.a,temp.b);
            //system("pause");
        }

        temp.a=-temp.a;
        temp.b*=C[i+1][i];
        //printf("%I64d %I64d\n",temp.a,temp.b);
        //system("pause");

        //printf("%I64d\n",gcd(temp.a,temp.b));
        if(temp.a)
        {
            ll te=gcd(temp.a,temp.b);
            temp.a/=te;
            temp.b/=te;
        }
        else
            temp.b=0;
        B[i]=temp;
        //printf("i:%d %I64d %I64d\n",i,B[i].a,B[i].b);
        //system("pause");
    }
}

int main()
{
   //freopen("in.txt","r",stdin);
   //freopen("out.txt","w",stdout);

   //printf("%I64d\n",gcd(-6,12));

   init();
   while(~scanf("%I64d",&k))
   {

       ll cur=1;

       for(int i=0;i<=k;i++)
       {
           if(i==1)
           {
               ans[i].a=k+1;  //B[1]=-1/2要加上后面多出来的n^k
               ans[i].b=2;
           }
           else
           {
               ans[i]=B[i];
               ans[i].a*=C[k+1][i];
           }

           if(ans[i].a) //约分
           {
               ll temp=gcd(ans[i].a,ans[i].b);
               ans[i].a/=temp;
               ans[i].b/=temp;
           }
           else
                ans[i].b=0;
           if(ans[i].b) //求分母的最小公倍数
                cur=cur/gcd(cur,ans[i].b)*ans[i].b;

       }
       printf("%I64d ",cur*(k+1));
       //printf("->%I64d %I64d %I64d\n",cur,ans[0].a,ans[0].b);
       for(int i=0;i<=k;i++) //求出通分后每个系数
       {
           if(ans[i].b)
               ans[i].a=cur/ans[i].b*ans[i].a;
               //printf("i:%d %I64d\n",i,ans[i].a);
       }
       for(int i=0;i<=k;i++)
            printf("%I64d ",ans[i].a);
       printf("0\n"); //最后一个肯定是0
   }
   return 0;
}