CCPC-Wannafly Winter Camp Day8 (Div2, onsite) A 题 Aqours （精巧的树形DP）

题目链接： https://www.cometoj.com/contest/29/problem/A?problem_id=414

Aqours

题目描述

Aqours 正在 LoveLive! 决赛中表演，舞台可以看作是一棵 nn 个点的有根树，其中根节点是 1 号点，ii 号点的父亲节点为 p_ip

i

​

，保证 1 \le p_i < i1≤p

i

​

<i，而且对于 2 \le i < j \le n2≤i<j≤n 有 p_i \le p_jp

i

​

≤p

j

​

。

其中的叶子节点（定义为没有孩子节点的点）是与粉丝进行互动的节点，Aqours 会在这些叶子节点之间走动来与更多的粉丝互动，但是她们又要唱歌又要跳舞，要尽快节省走动时间，然后也要做到雨露均沾，所以每次要往编号更小的叶子节点走。

所以 Aqours 想知道对于每一个叶子节点 uu，离它最近的编号 < u<u 的叶子节点到它的距离是多少，若不存在则视距离为 -1。

输入描述

第一行一个正整数 n (1 \le n \le 3 \times 10^6)n(1≤n≤3×10

6

)，表示树的大小。

第二行 n-1n−1 个正整数，其中第 ii 个数表示 p_{i+1}(1 \le p_{i+1} \le i)p

i+1

​

(1≤p

i+1

​

≤i)。

对于 2 \le i < j \le n2≤i<j≤n，保证 p_i \le p_jp

i

​

≤p

j

​

。

输出描述

每个叶子对应的答案输出一行。每行第一个数是叶子节点的编号 uu，第二个数是离他最近的编号 < u<u 的叶子节点到它的距离，若不存在则输出 -1。

要求按叶子节点编号从小到大输出。

样例输入 1

10

1 1 1 1 2 4 5 6 7

样例输出 1

3 -1

8 3

9 4

10 4

思路：

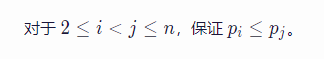
对于题面的这句话，我们可以把给定的点序列看为数的BFS序。

我们维护一个信息 dp[i] 代表距离第i个节点最近的叶子节点的距离。

我们从1到n，扫每一个叶子节点Y，我们向上（它的父节点）dfs，dfs过程中维护f的值，直到遇到一个已经访问（被其他节点dfs过得）的节点 X 。那么当前节点的答案就是 dp[X] +Y到X节点的步数。

同时还需要回溯更新dp[i] 的信息。

为什么正确？

1、我们是从1到n逐一扫描每一个叶子 节点Y，所以当一个叶子节点向上dfs的过程中遇到了一个已经放过的节点X时，X节点一定是被编号比Y小的节点更新的。所以保证了题目的要求。

2、我们在dfs过程中同时回溯维护dp[i] 的信息，就保证了dp[i] 即可以是其他节点通过先上后下到达的，也可以是下方的节点一直向上走到达的。

这样保证了dp[i] 的正确性。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define rt return
#define dll(x) scanf("%I64d",&x)
#define xll(x) printf("%I64d\n",x)
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2)ans = ans * a % MOD; a = a * a % MOD; b /= 2;} return ans;}
inline void getInt(int* p);
const int maxn = 3000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
int du[maxn];
int far[maxn];
bool vis[maxn];
int n;
int ans;
int dp[maxn];
int dfs(int id,int step)
{
    if(vis[id])
    {
        ans=dp[id]+step;
        return dp[id]+1;
    }else
    {
        int temp=inf;
        dp[id]=step;
        vis[id]=1;
        if(id!=1)
        {
            temp=dfs(far[id],step+1);
        }
        if(temp<dp[id])
            dp[id]=temp;
        return dp[id]+1;
    }
}
int main()
{
    //freopen("D:\\code\\text\\input.txt","r",stdin);
    //freopen("D:\\code\\text\\output.txt","w",stdout);
    gg(n);
    int x;
    repd(i,2,n)
    {
        gg(x);
        du[x]++;
        far[i]=x;
    }
    repd(i,1,n)
    {
        ans=-1;
        if(du[i]==0)
        {
            dfs(i,0);
            printf("%d %d\n",i,ans);
        }
    }

    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    }
    else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}