机器学习实战笔记-5-Logistic回归

Logistic回归

优缺点	适用范围
优点：计算代价不高，易于理解和实现。 缺点：容易欠拟合，分类精度可能不高。 适用于：数值型和标称型数据。	仅用于二分类

原理：

每个特征都乘以一个回归系数>>将结果相加>>总和代入到Sigmoid函数，得到范围在(0,1)中的数值>>预测分类结果\(\hat{y}\)。即\(Z= w_{0}x_{0} + w_{1}x_{1} + \ldots + w_{n}x_{n} = \sum_{i = 0}^{n}{w_{i}x_{i} =w^{T}x}\)，代入Sigmoid函数即可。

两个类别的分割点是\(Z=0\)，即直线\(w_{0}x_{0}+w_{1}x_{1}+\ldots +w_{n}x_{n}=0\)。

\[\sigma\left( Z \right) = \frac{1}{1 + e^{- Z} }\ \ \rightarrow \ \ y^{'} = \frac{1}{1 + e^{- \mathbf{w}^{T}\mathbf{x} } }\text{\ \ }\ \frac{1}{1 + e^{g\left( x \right)} }
\]

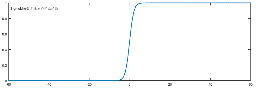
若用\(y’\)表示分类为1的概率，\(P\left( y = 1 \middle| x,w \right) =
y'\)，则分类为0的概率为\(P\left( y = 0 \middle| x,w \right) = 1 - y'\)。

极大似然概率为\(L\left( w \right) = \prod_{i =
1}^{m}{ { {(y}_{i}^{'})}^{y_{i} }\left( 1 - y_{i}^{'} \right)^{1 - y_{i} } }\)，

取对数后为\(\mathbf{l}\left( \mathbf{w} \right)\mathbf{=}\sum_{\mathbf{i =
1} }^{\mathbf{m} }{\mathbf{(}\mathbf{y}_{\mathbf{i} }\log\left(
\mathbf{y}^{\mathbf{'} } \right)\mathbf{+ (1
-}\mathbf{y}_{\mathbf{i} }\mathbf{)log(1
-}\mathbf{y}_{\mathbf{i} }^{\mathbf{'} }\mathbf{)} }\mathbf{)}\)，迭代式为

\(\mathbf{w}_{\mathbf{j} }\mathbf{: =}\mathbf{w}_{\mathbf{j} }\mathbf{+
\alpha}\frac{\mathbf{\partial} }{\mathbf{\partial}\mathbf{w}_{\mathbf{j} } }\mathbf{l(w)}\)

\[\frac{\partial}{\partial w_{j} }l\left( w \right) = \sum_{i = 1}^{m}{\left( y_{i}\frac{1}{y_{i}^{'} } + \left( 1 - y_{i} \right)\frac{1}{1 - y_{i}^{'} } \right)\frac{\partial}{\partial w_{j} }y_{i}^{'}\ } = \sum_{i = 1}^{m}{\left( y_{i}\frac{1}{y_{i}^{'} } + \left( 1 - y_{i} \right)\frac{1}{1 - y_{i}^{'} } \right)y_{i}^{'}\left( 1 - y_{i}^{'} \right)\frac{\partial}{\partial w_{j} }\mathbf{w}^{T}\mathbf{x}\ }
\]

\[= \sum_{i = 1}^{m}{\left( y_{i}\left( 1 - y_{i}^{'} \right) + \left( 1 - y_{i} \right)y_{i}^{'} \right)x_{i,j} } = \sum_{\mathbf{i = 1} }^{\mathbf{m} }{\mathbf{(}\mathbf{y}_{\mathbf{i} }\mathbf{-}\mathbf{y}_{\mathbf{i} }^{\mathbf{'} }\mathbf{)} }\mathbf{x}_{\mathbf{i,j} }
\]

其中用到了 记\(f\left( x \right) = \frac{1}{1 +
e^{g(x)} }\)，则\(\frac{\partial}{\partial x}f\left( x \right) = f\left( x
\right)\left( 1 - f\left( x \right) \right)\frac{\partial}{\partial x}g(x)\)

现有一数据集trainMat，记作矩阵X，则\(error = \mathbf{\text{labelMat} } -
\sigma(\mathbf{X} \times \mathbf{w})\)为预测值与实际值的差。

极大似然概率就是要回归的最大值\(l(w)\)，并不在代码中体现，迭代式为

\[w_{j} w_{j} + \alpha\frac{\partial}{\partial w_{j} }l\left( w \right) = w_{j} + \alpha \bullet \sum_{\mathbf{i = 1} }^{\mathbf{m} }{\mathbf{(}\mathbf{y}_{\mathbf{i} }\mathbf{-}\mathbf{y}_{\mathbf{i} }^{\mathbf{'} }\mathbf{)} }\mathbf{x}_{\mathbf{i,j} }
\]

\[\mathbf{w = w +}\alpha\mathbf{\bullet}\mathbf{x}^{\mathbf{T} }\mathbf{\times error}
\]

梯度上升算法伪代码：

  每个回归系数初始化为1
  重复R次
    计算整个数据集的梯度
    使用alpha×gradient更新回归系数的向量
  返回回归系数

随机梯度上升算法伪代码：

每个回归系数初始化为1
对数据集中每个样本
  计算该样本的梯度
  使用alpha×gradient更新回归系数的值
返回回归系数值

---

知识点：最大似然估计法-本质就是求联合概率的最大值

二项分布的似然函数(某次实验：投n次硬币有m次正面)

\[L\left( \theta \right) = C_{n}^{m}\theta^{m}\left( 1 - \theta \right)^{n - m}
\]

二项分布用通俗点的话来说，就是描述了抛10次硬币的结果的概率，其中，“花”出现的概率为\(\theta\)。如{4,5,5,2,7,4}就是6次实验的结果，每个数字表示抛10次硬币出现了几次“花”。

用\(x_{1},x_{2},\ldots,x_{n}\)表示实验结果，则因为每次实验都是独立的，所以似然函数可以写作（得到这个似然函数很简单，独立事件的联合概率，直接相乘就可以得到）:

\[L\left( \theta \right) = f\left( x_{1} \middle| \theta \right)f\left( x_{2} \middle| \theta \right)\ldots f\left( x_{n} \middle| \theta \right)
\]

其中\(f\left( x_{n} \middle| \theta\right)\)表示同一参数下的实验结果，也可认为是条件概率。

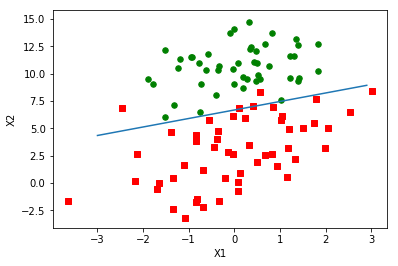
用python画的图