Java 计算两点间的全部路径（一）

算法要求：

1. 在一个无向连通图中求出两个给定点之间的所有路径；
2. 在所得路径上不能含有环路或重复的点；

算法思想描述：

1. 整理节点间的关系，为每个节点建立一个集合，该集合中保存所有与该节点直接相连的节点（不包括该节点自身）；
2. 定义两点一个为起始节点，另一个为终点，求解两者之间的所有路径的问题可以被分解为如下所述的子问题：对每一 个与起始节点直接相连的节点，求解它到终点的所有路径（路径上不包括起始节点）得到一个路径集合，将这些路径集合相加就可以得到起始节点到终点的所有路径；依次类推就可以应用递归的思想，层层递归直到终点，若发现希望得到的一条路径，则转储并打印输出；若发现环路，或发现死路，则停止寻路并返回；
3. 用栈保存当前已经寻到的路径（不是完整路径）上的节点，在每一次寻到完整路径时弹出栈顶节点；而在遇到从栈顶节点无法继续向下寻路时也弹出该栈顶节点，从而实现回溯。

代码实现

import java.util.ArrayList;

/* 表示一个节点以及和这个节点相连的所有节点 */
public class Node {
	public String name = null;
	public ArrayList<Node> relationNodes = new ArrayList<Node>();

	public String getName() {
		return name;
	}

	public void setName(String name) {
		this.name = name;
	}

	public ArrayList<Node> getRelationNodes() {
		return relationNodes;
	}

	public void setRelationNodes(ArrayList<Node> relationNodes) {
		this.relationNodes = relationNodes;
	}
}

import java.util.ArrayList;
import java.util.Iterator;
import java.util.Stack;

public class Test2 {
	/* 临时保存路径节点的栈 */
	public static Stack<Node> stack = new Stack<Node>();
	/* 存储路径的集合 */
	public static ArrayList<Object[]> sers = new ArrayList<Object[]>();

	/* 判断节点是否在栈中 */
	public static boolean isNodeInStack(Node node) {
		Iterator<Node> it = stack.iterator();
		while (it.hasNext()) {
			Node node1 = (Node) it.next();
			if (node == node1)
				return true;
		}
		return false;
	}

	/* 此时栈中的节点组成一条所求路径，转储并打印输出 */
	public static void showAndSavePath() {
		Object[] o = stack.toArray();
		for (int i = 0; i < o.length; i++) {
			Node nNode = (Node) o[i];

			if (i < (o.length - 1))
				System.out.print(nNode.getName() + "->");
			else
				System.out.print(nNode.getName());
		}
		sers.add(o); /* 转储 */
		System.out.println("\n");
	}

	/*
	 * 寻找路径的方法 cNode: 当前的起始节点currentNode pNode: 当前起始节点的上一节点previousNode sNode:
	 * 最初的起始节点startNode eNode: 终点endNode
	 */
	public static boolean getPaths(Node cNode, Node pNode, Node sNode, Node eNode) {
		Node nNode = null;
		/* 如果符合条件判断说明出现环路，不能再顺着该路径继续寻路，返回false */
		if (cNode != null && pNode != null && cNode == pNode)
			return false;

		if (cNode != null) {
			int i = 0;
			/* 起始节点入栈 */
			stack.push(cNode);
			/* 如果该起始节点就是终点，说明找到一条路径 */
			if (cNode == eNode) {
				/* 转储并打印输出该路径，返回true */
				showAndSavePath();
				return true;
			}
			/* 如果不是,继续寻路 */
			else {
				/*
				 * 从与当前起始节点cNode有连接关系的节点集中按顺序遍历得到一个节点 作为下一次递归寻路时的起始节点
				 */
				nNode = cNode.getRelationNodes().get(i);
				while (nNode != null) {
					/*
					 * 如果nNode是最初的起始节点或者nNode就是cNode的上一节点或者nNode已经在栈中 ， 说明产生环路
					 * ，应重新在与当前起始节点有连接关系的节点集中寻找nNode
					 */
					if (pNode != null && (nNode == sNode || nNode == pNode || isNodeInStack(nNode))) {
						i++;
						if (i >= cNode.getRelationNodes().size())
							nNode = null;
						else
							nNode = cNode.getRelationNodes().get(i);
						continue;
					}
					/* 以nNode为新的起始节点，当前起始节点cNode为上一节点，递归调用寻路方法 */
					if (getPaths(nNode, cNode, sNode, eNode))/* 递归调用 */
					{
						/* 如果找到一条路径，则弹出栈顶节点 */
						stack.pop();
					}
					/* 继续在与cNode有连接关系的节点集中测试nNode */
					i++;
					if (i >= cNode.getRelationNodes().size())
						nNode = null;
					else
						nNode = cNode.getRelationNodes().get(i);
				}
				/*
				 * 当遍历完所有与cNode有连接关系的节点后， 说明在以cNode为起始节点到终点的路径已经全部找到
				 */
				stack.pop();
				return false;
			}
		} else
			return false;
	}

	public static void main(String[] args) {
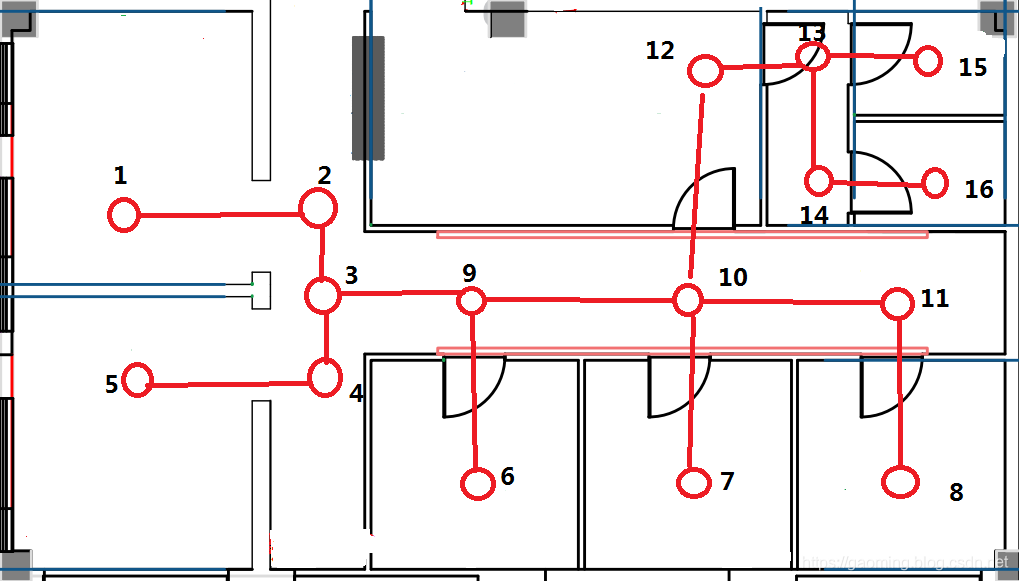
		/* 定义节点关系 */
		String nodeRalation[][] = { { "0" }, // 0
				{ "2" }, // 1
				{ "1", "3" }, // 2
				{ "2", "4", "9" }, // 3
				{ "3", "5" }, // 4
				{ "4" }, // 5
				{ "9" }, // 6
				{ "10", "8" }, // 7
				{ "7", "11" }, // 8
				{ "3", "6", "10" }, // 9
				{ "9", "7", "11" }, // 10
				{ "10", "8" } // 11
		};

		/* 定义节点数组 */
		Node[] node = new Node[nodeRalation.length];

		for (int i = 0; i < nodeRalation.length; i++) {
			node[i] = new Node();
			node[i].setName("node" + i);
		}

		/* 定义与节点相关联的节点集合 */
		for (int i = 0; i < nodeRalation.length; i++) {
			ArrayList<Node> List = new ArrayList<Node>();

			for (int j = 0; j < nodeRalation[i].length; j++) {
				for (int z = 0; z < nodeRalation.length; z++) {
					if (node[z].getName().equals("node" + nodeRalation[i][j])) {
						List.add(node[z]);
						break;
					}
				}
			}
			node[i].setRelationNodes(List);
			List = null; // 释放内存
		}

		/* 开始搜索所有路径 */
		getPaths(node[1], null, null, node[8]);
	}
}

node1->node2->node3->node9->node10->node7->node8

node1->node2->node3->node9->node10->node11->node8