[CSP-S模拟测试]:幻魔皇（数学）

题目描述

　　幻魔皇拉比艾尔很喜欢斐波那契树，他想找到神奇的节点对。
　　所谓斐波那契树，根是一个白色节点，每个白色节点都有一个黑色节点儿子，而每个黑色节点则有一个白色和一个黑色节点儿子。神奇的节点对则是指白色节点对。
　　请问对于深度为$n$的斐波那契树，其中距离为$i$的神奇节点对有多少个？拉比艾尔需要你对于$1\leqslant i\leqslant 2n$的所有$i$都求出答案。

---

输入格式

一行一个正整数$n$。

---

输出格式

一行$2n$个整数表示答案，对$123456789$取模。

---

样例

样例输入：

5

样例输出：

0 2 3 3 1 1 1 0 0 0 0

---

数据范围与提示

对于$20\%$的数据$n\leqslant 10$；
对于$40\%$的数据$n\leqslant 20$；
对于$60\%$的数据$n\leqslant 30$；
对于$80\%$的数据$n\leqslant 400$；
对于$100\%$的数据$n\leqslant 5,000$。

---

题解

先来看一下这棵树：

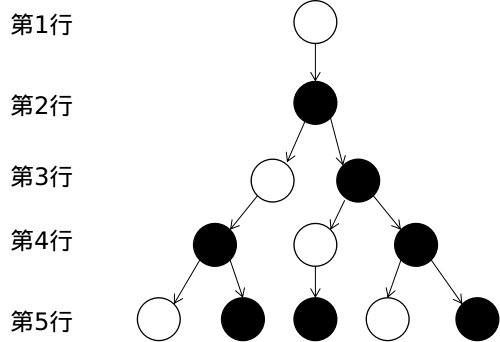
首先，来看几点性质：

　　$\alpha.$每一行的点数呈斐波那契数列。

　　$\beta.$从第二行开始，每行的黑点个数呈斐波那契数列。

　　$\gamma.$从第三行开始，每行的白点个数呈斐波那契数列。

　　$\delta.$对于每一个黑（白）点，如果它有一棵深度为$k$的子树，那么所有这些子树都是一样的。

得到了这些性质，再来看这道题：

设$w[i]$表示第$i$行的白点的个数，$b[i]$表示第$i$行黑点的个数，$sw[i]$表示小于等于$i$行的所有白点的个数，$sb[i]$表示小于等于$i$行的所有黑点的个数（注意此处的行数其实也是深度，根节点的深度为$1$）。

思考如何计数，根据性质$\delta$，可以考虑将每一棵不同的子树内部贡献，再乘上这样子树的数量即可得到答案。

再来考虑如何统计子树内部的贡献，可以大致分为两种情况：

　　$\alpha.$神奇节点对的$LCA$为白色点。

　　$\beta.$神奇节点对的$LCA$为黑色点。

观察上面的图可知，对于情况$\alpha$，$LCA$一定是其中一个白点，就是说这两个白点一定是祖先和后代的关系。

那么，对于一个深度为$k$的子树，其贡献为$w[i+1]$（因为祖先白点的行数是$1$），而这样的子树有$sw[n-i]$棵。

所以，对于情况$\alpha$，其对答案的贡献即为：

$$\sum \limits_{i=1}^n sw[n-i]\times w[i+1]$$

对于情况$\beta$，就显得麻烦很多了，两个白点必须在这个黑点（$LCA$）的两个子节点的子树中。

考虑枚举两侧的距这个黑点的距离$i,j$（白色子节点的子树中的白点的距离为$i$，黑色子节点的子树中的白点的距离为$j$），并将这棵树进行如下图所示划分：

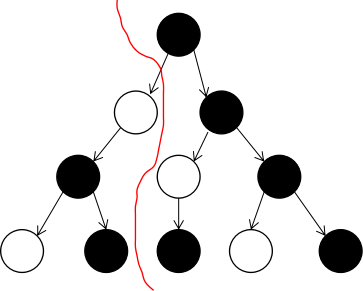
惊喜的发现，如果将右侧树的根节点由黑变白对答案没有影响，而右侧树就变成了一棵深度为$j+1$的普通树，那么其距离为$j$的白点就有$w[j+1]$个。

左侧深度为$i+1$，则对于左侧树其深度为$i$，所以距离为$i$的白点个数为$w[i]$。

那么对于这棵树，其对答案的贡献就是$w[i]\times w[j+1]$，而这样的子树的数量取决与$i,j$中更大的那一个，所以这样的子树有$sb[n-\max(i,j)]$棵。

所以，对于情况$\beta$，其对答案的贡献即为：

$$\sum \limits_{i=1}^n \sum \limits_{j=1}^n sb[n-\max(i,j)]\times w[i]\times w[j+1]$$

时间复杂度：$\Theta(n^2)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
const int mod=123456789;
int n;
long long w[5001],b[5001],sw[5001],sb[5001];
long long ans[10001];
int main()
{
	scanf("%d",&n);
	w[1]=w[3]=1;
	sw[1]=sw[2]=1;sw[3]=2;
	for(int i=4;i<=n;i++)
	{
		w[i]=(w[i-1]+w[i-2])%mod;
		sw[i]=(sw[i-1]+w[i])%mod;
	}
	b[2]=1;sb[2]=1;
	for(int i=3;i<=n;i++)
	{
		b[i]=(b[i-1]+b[i-2])%mod;
		sb[i]=(sb[i-1]+b[i])%mod;
	}
	for(int i=1;i<=n;i++)
		ans[i]=sw[n-i]*w[i+1]%mod;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			ans[i+j]=(ans[i+j]+sb[n-max(i,j)]*w[i]%mod*w[j+1])%mod;
	for(int i=1;i<=2*n;i++)printf("%lld ",ans[i]);
	return 0;
}

---

rp++