Codeforces 1091C (数学)

题面

传送门

分析

假设k是固定的，那访问到的节点编号就是\(1+(a·k \mod n )\)，其中a为正整数。

通过找规律不难发现会出现循环。

通过题目中的图片我们不难发现

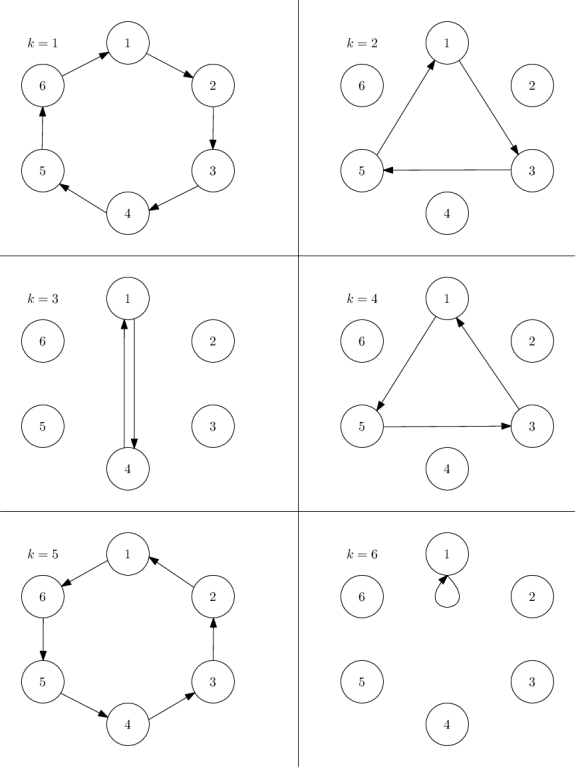
只有k=1,2,3,6得到的四种结果，而其他的情况都和这4种结果的某种一样

所以我们只要考虑n的因数即可

对于固定的k我们发现访问到的节点为1,1+k,1+2k.....n-k+1,一共\(\frac{n}{k}\) 项，根据等差数列求和公式和为\(\frac{n(n-k+2)}{2k}\)

所以我们只要在\(O(\sqrt n)\)的时间内分解因数，然后再\(O(1)\)更新答案即可

代码

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#define maxn 100005
using namespace std;
long long n,k;
long long a[maxn];
int cnt=0;
vector<long long>ans;
void div(long long n){
	for(long long i=2;i*i<=n;i++){
		if(n%i==0){
			a[++cnt]=i;
			if(i!=n/i) a[++cnt]=n/i;
		}
	}
}
int main(){
	scanf("%I64d",&n);
	div(n);
	for(int i=1;i<=cnt;i++){
		long long x=a[i];
		long long f=n/x*(n-x+2)/2;
		ans.push_back(f);
	}
	sort(ans.begin(),ans.end());
	for(int i=0;i<ans.size();i++){
		printf("%I64d ",ans[i]);
	}
}