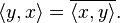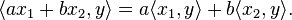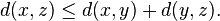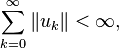Hilbert space

Definition

A Hilbert space H is a real or complex inner product space that is also a complete metric space with respect to the distance function induced by the inner product.^[2]
To say that H is a complex inner product space means that H is a complex vector space on which there is an inner product
associating a complex number to each pair of elements
x,y of H that satisfies the following properties:

• The inner product of a pair of elements is equal to the complex conjugate of the inner product of the swapped elements:

• The inner product is linear in its first argument.^[3] For all complex numbers
  a and b,

• The inner product of an element with itself is positive definite:

where the case of equality holds precisely when x = 0.

It follows from properties 1 and 2 that a complex inner product is antilinear in its second argument, meaning that

A real inner product space is defined in the same way, except that H is a real vector space and the inner product takes real values. Such an inner product will be bilinear: that is, linear in each argument.

The norm is the real-valued function

and the distance d between two points x,y in H is defined in terms of the norm by

That this function is a distance function means (1) that it is symmetric in
x and y, (2) that the distance between x and itself is zero, and otherwise the distance between
x and y must be positive, and (3) that the triangle inequality holds, meaning that the length of one leg of a triangle
xyz cannot exceed the sum of the lengths of the other two legs:

This last property is ultimately a consequence of the more fundamental Cauchy–Schwarz inequality, which asserts

with equality if and only if x and y are linearly dependent.

Relative to a distance function defined in this way, any inner product space is a
metric space, and sometimes is known as a pre-Hilbert space.^[4] Any pre-Hilbert
space that is additionally also a complete space is a Hilbert space. Completeness is expressed using a form of the
Cauchy criterion for sequences in H: a pre-Hilbert space H is complete if every
Cauchy sequence converges with respect to this norm to an element in the space. Completeness can be characterized by the following equivalent condition: if a series of vectors

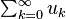
converges absolutely in the sense that

then the series converges in H, in the sense that the partial sums converge to an element of
H.

As a complete normed space, Hilbert spaces are by definition also Banach spaces. As such they are topological vector spaces, in which topological notions like the openness and closedness of subsets are well-defined. Of special importance is the notion of a closed
linear subspace of a Hilbert space that, with the inner product induced by restriction, is also complete (being a closed set in a complete metric space) and therefore a Hilbert space in its own right.

摘自：https://en.wikipedia.org/wiki/Hilbert_space