POJ——3264线段树

题目：

输入两个数（m,n）,m表示牛的头数，n表示查询的个数。
查询时输入两个数（x,y），表示查询范围的起始值和终止值，查询结果是，这个区间内牛重量的最大值减去牛重量的最小值，数量级为1000,000 设计每次查询的复杂度为logm。

例如，

输入：

6 3
1
7
3
4
2
5
1 5
4 6
2 2

输出：

6
3
0

---

分析：这道题是典型的空间换时间的题。一看到是区间的查找，我们应该想到线段树，这里有一篇我觉得写得挺好的介绍线段树的博客和大家分享一下：http://www.cnblogs.com/shuaiwhu/archive/2012/04/22/2464583.html。

1.根据输入m值，建立线段树。public void buildTree(int m) 

2.根据输入的牛的体重，初始化线段树。public void initTree(SNode sn, int value)

3.根据查询，查询线段树。public void find(SNode sn, int a, int b)

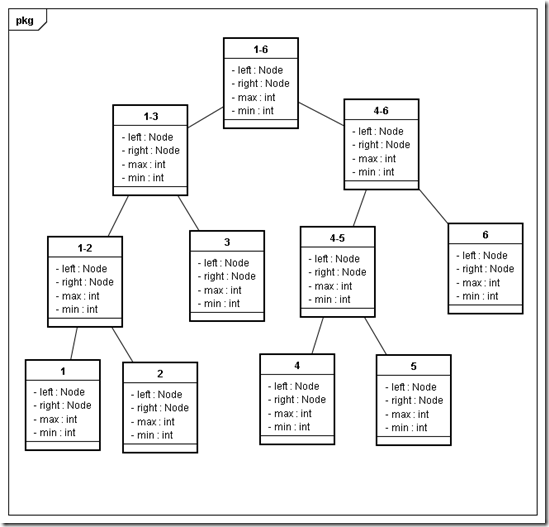
首先我们来看建立线段树。由于要查询的是最大值与最小值之差，所以在线段树中每个结点除了要存储范围的左右阈值和左右子节点的引用外，还要存储该区间内的最大值最小值。以6头牛为例，设编号为1-6，那么最终构建的线段树应该如下图所示：

分析一下建树的递归过程。

首先，终止条件是：first==last（以结点1为例，那么，first=1，last=1）；

然后，递归的共同操作是：为结点中的first和last赋值，表明结点的范围，即

node.first = first，node.last = last；

接着，看递归的参数：通过前面的分析可知，肯定有一个结点引用的参数node，然后因该要有结点的范围，即first和last；

最后，看递归的过程：递归的过程无非就是左右子树递归，即：

node.left = new SNode();
node.right = new SNode();
build(node.left, first, ( first + last) / 2);
build(node.right, ( first + last) / 2 + 1, last);

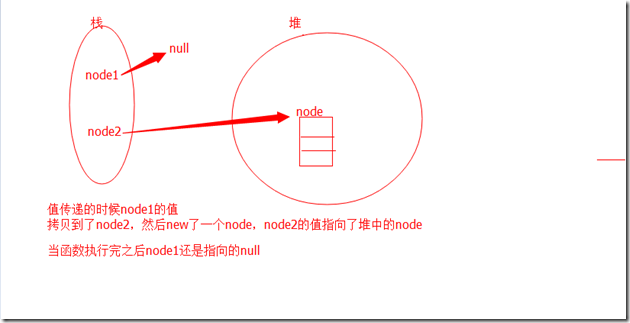
在这里注意：为什么要先给左右子节点的引用赋值，因为在java中，不先给赋值的话，没有分配指向的地址，参数传递之后，是对参数进行的赋值，返回之后原结点还是指向null的。下图分析这个值传递的过程：

node1先new的过程就相当于node1先指向了堆中的node，然后，node1拷贝到node2，node2也指向node，那么用node2修改node和node1修改node就是一样的效果。

理解了建立线段树的过程，后面初始化线段树和查找的过程也是类似的方法，这里就不详述了，直接上代码吧。

---

代码：

package study;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

/**
 * http://poj.org/problem?id=3264

 * 输入两个数（m,n）,m表示牛的头数，n表示查询的个数。
 * 查询结构如下（x,y），这个区间内牛重量的最大值减去，牛重量的最小值，为查询结果， 数量级为100,0000 设计每次查询的复杂度为logm。
 *
 * @author cnx
 * @CreateDate ; 2014年9月28日 下午9:38:25
 */
public class SegmentTree {
    public static void main(String[] args) throws IOException {
        SegmentTree s = new SegmentTree();
        BufferedReader stdin = new BufferedReader(new InputStreamReader(
                System.in));

        String line = stdin.readLine();
        StringTokenizer st = new StringTokenizer(line);
        s.m = Integer.parseInt(st.nextToken());
        s.n = Integer.parseInt(st.nextToken());
        //建树，并初始化结点
        s.buildTree(s.m);
        for (s.inc = 1; s.inc <= s.m; s.inc++) {
            line = stdin.readLine();
            st = new StringTokenizer(line);
            int value = Integer.parseInt(st.nextToken());
            s.initTree(s.sn, value);
        }
        //输入查询，并给出结果
        for (int i = 0; i < s.n; i++) {
            line = stdin.readLine();
            st = new StringTokenizer(line);
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            s.max = 0;
            s.min = 99999999;
            s.find(s.sn,a,b);

            System.out.println(s.max-s.min);
        }

    }

    public int m;
    public int n;
    public SNode sn = new SNode();

    public int inc;
    public int max;
    public int min;

    /**
     * 线段树结点类
     * @author cnx
     * @CreateDate ; 2014年9月29日 上午9:17:55
     */
    public static class SNode {
        int first;
        int last;
        int max;
        int min = 9999999;
        SNode left ;
        SNode right ;
    }
    /**
     * 构建线段树
     * @param m  范围为1-m
     */
    public void buildTree(int m) {
        build(sn, 1, m);
    }
    /**
     * 构建线段树的递归函数
     * @param node
     * @param L   线段树结点中的first，即范围的左阈值
     * @param R   结点中的last，即范围的右阈值
     */
    public void build(SNode node, int L, int R) {
        if(node == null)
            node = new SNode();
        node.first = L;
        node.last = R;
        if (L == R) {
            return;
        }

        node.left = new SNode();
        node.right = new SNode();
        build(node.left, L, (L + R) / 2);
        build(node.right, (L + R) / 2 + 1, R);
    }
    /**
     * 给线段树的max和min字段赋值
     * @param sn
     * @param value  输入的值
     */
    public void initTree(SNode sn, int value) {
        if (value > sn.max) {
            sn.max = value;
        }
        if (value < sn.min) {
            sn.min = value;
        }
        if (sn.first == sn.last) {
            return;
        }
        if (inc > (sn.last + sn.first) / 2) {
            initTree(sn.right, value);
        } else {
            initTree(sn.left, value);
        }
    }
    /**
     * 在线段树中查找，范围a-b的最大值和最小值
     * @param sn
     * @param a
     * @param b
     */
    public void find(SNode sn, int a, int b){

        if (sn.first==a && sn.last==b) {
            if (sn.max>max) {
                max = sn.max;
            }
            if (sn.min<min) {
                min = sn.min;
            }
            return;
        }

        if (b<=(sn.first+sn.last)/2) {
            find(sn.left, a, b);
        }
        else if (a>(sn.first+sn.last)/2) {
            find(sn.right, a, b);
        }
        else {
            find(sn.left, a, (sn.first+sn.last)/2);
            find(sn.right, (sn.first+sn.last)/2+1, b);
        }
    }

}