【转载】从零实现3D图像引擎：(2)画2D直线不简单

原文：从零实现3D图像引擎：(2)画2D直线不简单

1. 数学分析

1) 画直线的问题

本来我以为画直线会很容易，随便拿个直线公式，遍历X求Y画出来不就完了么，但事实并非如此。以2D直线为例，因为3D直线也只是多引入了个Z坐标而已。关键的问题：我们在数学中所学的直线是基于实数域的，而在计算机屏幕上，所画的直线是基于正整数域的，可以想象这么一个情形，在直线的某一点X=1，Y=0.01时，在屏幕上如何画呢？下图对比了实数域的直线，与基于正整数域的直线：

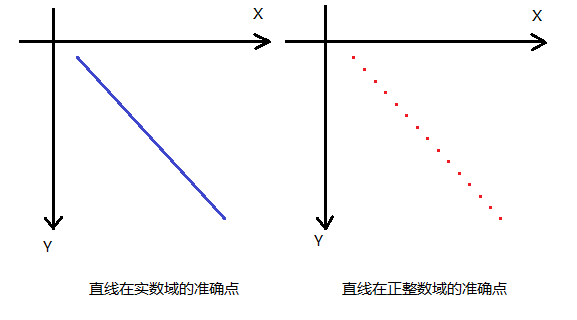
为什么直线在正整数域是不连续的呢，还记得斜率的的定义么：斜率m = dy / dx = (y1 - y0) / (x1 - x0)

这意味着当X坐标增加1，则Y坐标就增加m。这就是会出现上述情况的根本原因。

2) Bresenham算法

该算法由Bresenham在1965年发明，它到底做了什么事呢？其实想法很简单，就是每X移动一个像素，则考虑Y应该是如何移动。为什么我们要关注Bresenham算法呢，我们发现，这种算法实际只做了加减法，是非常适合计算机运算的，这种算法的速度是相当快的。

该算法把直线分为两种：一种是斜率<1的线，即近X轴线。另一种是斜率>1的线，即近Y轴线。

我们以近X轴直线为例，如图：

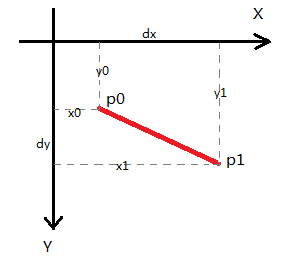
Bresenham算法的核心就是，当X加1后，如何决定Y的移动。显然可见，近X轴直线的dy<dx。所以一个直观的想法是，保存一个误差累计变量，每当X加1，误差变量便累计增加一个dy。当累计误差小于等于dx时，Y不动，当累计的误差大于dx时，Y加1，同时把累计误差减掉一个dx。这样，算法将不停的将光栅线与实际线之间的误差减到最小。

2. 函数实现

这里给出一个例子，实现了上面的算法，但只限近X轴并且是从左上往右下画的，可以很清楚的看到实现的逻辑。通用的画线在源码中已实现，可以下载获取。

int dx = x1 - x0;
int dy = y1 - y0;
int error = 0;
if (dx > dy) // 近X轴
{
	for (int x = x0, y = y0; x<= x1; ++x)
	{
		DrawPixel(x, y, color);
		error += dy; // 累计误差

		if (error > dx)
		{
			error -= dx;
			++y;
		}
	}
}

　　针对所有情况的完整代码如下，其中在误差的计算方面进行了一些优化，起始值更居中，而不是写死的0。

int _CPPYIN_3DLib::DrawLine(int x0, int y0, int x1, int y1, DWORD color)
{
	int x, y, dx, dy, dx2, dy2, xstep, ystep, error, index;
	x = x0;
	y = y0;
	dx = x1 - x0;
	dy = y1 - y0;

	if (dx >= 0) // 从左往右画
	{
		xstep = 1; // x步进正1
	}
	else // 从右往左画
	{
		xstep = -1; // x步进负1
		dx = -dx; // 取绝对值
	}

	if (dy >= 0) // 从上往下画
	{
		ystep = 1; // y步进正1
	}
	else // 从下往上画
	{
		ystep = -1; // y步进负1
		dy = -dy; // 取绝对值
	}

	dx2 = dx << 1; // 2 * dx
	dy2 = dy << 1; // 2 * dy

	if (dx > dy) // 近X轴直线
	{
		error = dy2 - dx;
		for (index = 0; index <= dx; ++index)
		{
			DrawPixel(x, y, color);
			if (error >= 0)
			{
				error -= dx2;
				y += ystep;
			}
			error += dy2;
			x += xstep;
		}
	}
	else // 近Y轴直线
	{
		error = dx2 - dy;
		for (index = 0; index <= dy; ++index)
		{
			DrawPixel(x, y, color);
			if (error >= 0)
			{
				error -= dy2;
				x += xstep;
			}
			error += dx2;
			y += ystep;
		}
	}

	return 1;
}

　　

3. 源码下载

这个示例使用该函数，每帧在窗口中画500条随机颜色的直线，截图如下：

项目源代码下载：>>点击进入下载页<<

4. 补充更新

画直线还有一些算法，速度有的更快，如：

Run-Slicing

Symmetric Double Step

Quadruple Step

如果有时间我会一一实现，如果读者已经实现，请留言分享，谢谢。