【NOI2008】假面舞会

题目描述

一年一度的假面舞会又开始了，栋栋也兴致勃勃的参加了今年的舞会。

今年的面具都是主办方特别定制的。每个参加舞会的人都可以在入场时选择一 个自己喜欢的面具。每个面具都有一个编号，主办方会把此编号告诉拿该面具的人。

为了使舞会更有神秘感，主办方把面具分为\(k (k \ge 3)\)类，并使用特殊的技术将每个面具的编号标在了面具上，只有戴第$i \(类面具的人才能看到戴第\)i+1$ 类面具的人的编号，戴第$k $类面具的人能看到戴第\(1\) 类面具的人的编号。

参加舞会的人并不知道有多少类面具，但是栋栋对此却特别好奇，他想自己算出有多少类面具，于是他开始在人群中收集信息。

栋栋收集的信息都是戴第几号面具的人看到了第几号面具的编号。如戴第2号面具的人看到了第5 号面具的编号。栋栋自己也会看到一些编号，他也会根据自己的面具编号把信息补充进去。

由于并不是每个人都能记住自己所看到的全部编号，因此，栋栋收集的信 息不能保证其完整性。现在请你计算，按照栋栋目前得到的信息，至多和至少有多少类面具。由于主办方已经声明了\(k \ge 3\)，所以你必须将这条信息也考虑进去。

输入输出格式

输入格式

第一行包含两个整数\(n\), \(m\)，用一个空格分隔，\(n\) 表示主办方总共准备了多少个面具，\(m\) 表示栋栋收集了多少条信息。接下来\(m\) 行，每行为两个用空格分开的整数\(a\), \(b\)，表示戴第\(a\) 号面具的人看到了第\(b\) 号面具的编号。相同的数对\(a\), \(b\) 在输入文件中可能出现多次。

输出格式

包含两个数，第一个数为最大可能的面具类数，第二个数为最小可能的面具类数。如果无法将所有的面具分为至少\(3\) 类，使得这些信息都满足，则认为栋栋收集的信息有错误，输出两个\(-1\)。

题解

很明显我们需要考虑环和链：对于链来说无论这条链有多长，所允许的面具的个数都是任意的（注意：最小要为3）；对于一个环来说最多的面具数一定是这个环的大小，而且，当面具的个数为该环长的约数时也是符合要求的。

根据以上两点，我们就能够很轻松地想出我们的答案可以分为两类：一类是只有链的，就是最长链的长度和3了；另一类就是要考虑有环的情况，就是所有环的环长的最大公约数和大于3的最小公约数。而当最大答案都小于3的时候就是无解了。

建图技巧

我们需要Get到每个环的环长和链的链长，有下述的建图技巧：

我们可以把每条有向边\((u, v)\)分成两条，一条是\((u,v)\)权值为\(1\)， 一条是\((v, u)\)权值为\(-1\), 而这样的两条边有什么好处呢？这样我们就可以方便求出无环图的链长和环长了。

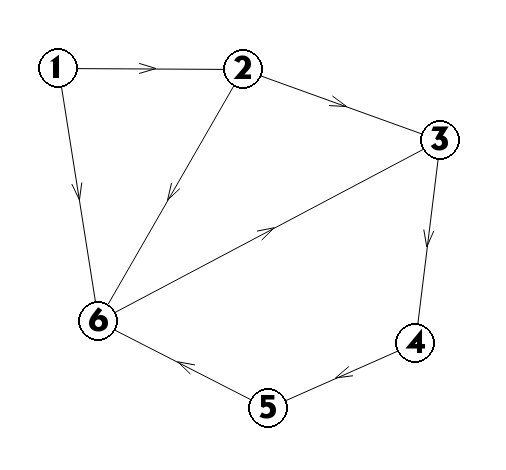
比如说下图：



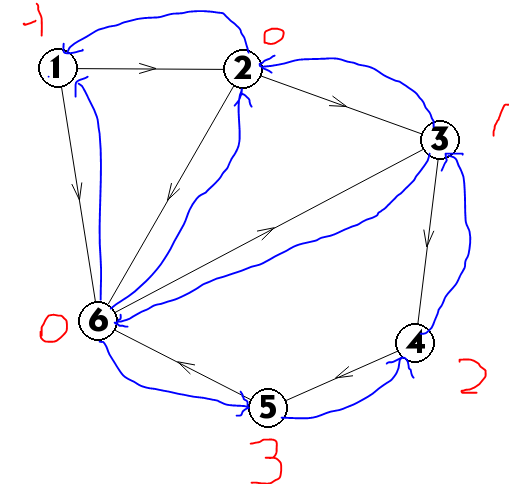
按照上面说的建图方式，我们可以得到这样的图（黑边权值为1，蓝边为-1）：



然后我们按照 \(2 \Rightarrow 1 \Rightarrow 6 \Rightarrow 3 \Rightarrow 4 \Rightarrow 5\) 的顺序遍历然后把每个点的点权记作\(p_i\), 令\(p_2 = 0\) 于是，我们可以得到如图所示的点权（红色数字），这样，当我们遍历到\(5\)时我们发现了一条边\((5, 6)\) 可以到结点 \(6\) ,而 \(6\) 我们已经遍历过了，证明有环，而环长就应该为 $abs(p_5 - p_6 + len（5， 6）) =abs(3 - 0 + 1) = 4 $

求链长也同理的，对于一个无环图，最长链即为\(p_{max} - p_{min} + 1\)

代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100005, MAXM = 1000005;

inline int gcd(int a, int b)
	{
		return !b ? a : gcd(b, a % b);
	}

int Head[MAXN], Next[MAXM << 1], To[MAXM << 1], w[MAXM << 1], edgenum;
inline void Add_edge(int from, int to, int cost)
	{
		Next[++ edgenum] = Head[from], Head[from] = edgenum, To[edgenum] = to, w[edgenum] = cost;
	}

int minn[MAXN], maxn[MAXN], p[MAXN], vis[MAXN], root;
int ans = 0;
inline void dfs(int u)
	{
		minn[root] = min(minn[root], p[u]), maxn[root] = max(maxn[root], p[u]), vis[u] = 1;
		for(int i = Head[u]; i != -1; i = Next[i])
			{
				int v = To[i];
				if(vis[v]) ans = gcd(ans, abs(p[u] - p[v] + w[i]));
				else{
					p[v] = p[u] + w[i];
					dfs(v);
				}
			}
	}

int fa[MAXN];
inline int find(int x)
	{
		return x == fa[x] ? x : fa[x] = find(fa[x]);
	} 

int main()
{
	int n, m, ans1 = 0, ans2 = 0;
	memset(Head, -1, sizeof(Head));
	memset(minn, 0x3f, sizeof(minn));

	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; ++ i) fa[i] = i;
	int x, y;
	for(int i = 1; i <= m; ++ i)
		{
			scanf("%d%d", &x, &y);
			Add_edge(x, y, 1), Add_edge(y, x, -1);
			x = find(x), y = find(y);
			if(x != y)	fa[x] = y;
		}
	for(int i = 1; i <= n; ++ i)
		if(!vis[i])
			{
				root = find(i);
				dfs(root);
			}
	ans1 = ans;
	for(int i = 3; i <= ans1; ++ i)
		if(! (ans1 % i))
			{
				ans2 = i; break;
			}
	if(ans2 < 3) ans2 = 3;
	root = 0;
	if(ans1 == 0)
		for(int i = 1; i <= n; ++ i)
			if(fa[i] == i)
				root += maxn[i] - minn[i] + 1;
	if(ans1 == 0)	ans1 = root;
	if(ans1 < 3) ans1 = ans2 = -1;
	printf("%d %d\n", ans1, ans2);
	return 0;
}