codeforces 1027 E. Inverse coloring (DP)

E. Inverse Coloring

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a square board, consisting of $$$n$$$ rows and $$$n$$$ columns. Each tile in it should be colored either white or black.

Let's call some coloring beautiful if each pair of adjacent rows are either the same or different in every position. The same condition should be held for the columns as well.

Let's call some coloring suitable if it is beautiful and there is no rectangle of the single color, consisting of at least $$$k$$$ tiles.

Your task is to count the number of suitable colorings of the board of the given size.

Since the answer can be very large, print it modulo $$$998244353$$$.

Input

A single line contains two integers $$$n$$$ and $$$k$$$ ($$$1 \le n \le 500$$$, $$$1 \le k \le n^2$$$) — the number of rows and columns of the board and the maximum number of tiles inside the rectangle of the single color, respectively.

Output

Print a single integer — the number of suitable colorings of the board of the given size modulo $$$998244353$$$.

Examples

Input

1 1

Output

0

Input

2 3

Output

6

Input

49 1808

Output

359087121

Note

Board of size $$$1 \times 1$$$ is either a single black tile or a single white tile. Both of them include a rectangle of a single color, consisting of $$$1$$$ tile.

Here are the beautiful colorings of a board of size $$$2 \times 2$$$ that don't include rectangles of a single color, consisting of at least $$$3$$$ tiles:

The rest of beautiful colorings of a board of size $$$2 \times 2$$$ are the following:

题意

矩阵的方格可以是黑色或白色，求满足条件的矩阵个数：相邻两列/行的颜色要么完全相同，要么完全相反，并且连续的黑色/白色的区域面积必须小于$$$K$$$

分析

假设现在已经有一个满足条件的矩阵，那么以第一行为基准，所有行要么和它相同，要么相反，如果用0/1分别表示相反/相同的话，从第一行到第n行就可以表示为一个长度为n的0/1序列，同理第一列到第n列也可以表示为长度为n的0/1序列。
当同时知道了行的0/1序列和列的0/1序列，只要再知道矩阵任何一个方格的颜色，就能唯一的表示一个矩阵了。

观察发现，同一种颜色的区域都是矩形，而且它们的大小来自于行和列上连续的0或1。如果把行和列的序列连续的0/1的个数记录下来，比如上面的例子中，行是2,3,3，列是1,2,2,1,2，我们就得到了两个新的序列，并且两个序列的数相乘就是所有色块的面积。
         
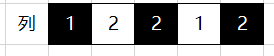
自然想到，行中最大的数乘以列中最大的数小于k就是充分必要条件，于是转而分析序列的最大值。
不难发现，序列的最大值可以从1取到n，如果已经知道最大值分别为1,2,3,..n的序列的个数，那么我们只需要让两个序列的最大值两两匹配，遍历所有乘积小于k的情况，就能求出总方案个数。
接下来的问题就是怎么取求最大值分别为1,2,3,..n的序列的个数，也就是说需要解决怎么求最大值为m，和为n的序列的个数。
假设用$$$(n,m)$$$代表最大值为$$$m$$$和为$$$n$$$的任意序列$$$a_1,a_2,...,a_t$$$，注意序列每个数字其实是有颜色的，那么总可以在$$$a_1$$$前面，添加一个颜色相反的数字$$$a_0$$$，如果它不大于$$$m$$$，那么就得到了一个$$$(n+a_0,m)$$$，按照这个思路，如果用$$$dp[n][m]$$$表示序列的个数，可以构造出状态转移方程：
$$$dp[n][m]=dp[n-1][m]+dp[n-2][m]+...+dp[n-m][m]$$$
含义就是$$$(n,m)$$$可以通过在$$$(n-1,m)$$$前面添加$$$1$$$，$$$(n-2,m)$$$前面添加$$$2$$$，...，的方法得到。
注意到一件事，$$$dp[n][m]$$$，当$$$n$$$小于等于$$$m$$$的时候，含义就是和为$$$n$$$的序列，且没有任何限制，那么个数就是$$$2^n$$$
所以状态转移方程就是：
$$$$$$dp[n][m]=
\begin{cases}
\sum_{i=1}^{m} dp[n-i][m], & {n\gt m} \\[2ex]
2^n, & {n\le m}
\end{cases}
$$$$$$
进一步发现，对于$$$n>m$$$的部分
$$$$$$\begin{align}
dp[n][m] &=dp[n-1][m]+dp[n-2][m]+...+dp[n-m][m]\\
&=dp[n-1][m]+(dp[n-1][m]-dp[n-m-1][m])\\
&=2*dp[n-1][m]-dp[n-m-1][m]
\end{align}$$$$$$
所以最终的状态转移方程就是：
$$$$$$dp[n][m]=
\begin{cases}
2*dp[n-1][m]-dp[n-m-1][m], & {n\gt m} \\[2ex]
2^n, & {n\le m}
\end{cases}
$$$$$$

总结

最开始的时候推了错的转移方程，$$$dp[n][m]=dp[n-m][m]+dp[n][m-1]$$$，发现得到的仅仅是组合的个数，并不是序列的个数，分析一下发现，这个转移方程相当于限定了序列必须是递减的，和正确的转移方程差了很多中间项

代码

#include<stdio.h>
typedef long long LL;
#define mod 998244353
int dp[][];
#define min(a,b) ((a)<(b)?(a):(b))
inline void add(int &a, int b) { a += b; if (a>mod)a -= mod; if (a<)a += mod; }

void init() {
    int temp;
    dp[][] = ; dp[][] = ;
    for (int t = ; t <= ; ++t) {
        dp[t][t] = (dp[t - ][t - ] << ) % mod;
        dp[][t] = ;
    }
    for (int k = ; k <= ; ++k) {
        for(int n=;n<=k;++n){
            dp[n][k] = dp[n][n];
        }
        for (int n = k + ; n <= ; ++n) {
            dp[n][k] = (*dp[n-][k]%mod-dp[n-k-][k]+mod)%mod;
        }
    }
}

int main() {
    int n, k;
    init();
    scanf("%d %d", &n, &k);
    int ans = ;
    LL help;
    for (int i = ; i <= n; ++i) {
        help = dp[n][i] - dp[n][i - ];
        help = help*(dp[n][min((k - ) / i,n)]) % mod;
        add(ans, help);
    }
    ans = (ans<<) % mod;
    printf("%d\n", ans);
}