【bzoj4002】[JLOI2015]有意义的字符串 数论+矩阵乘法

题目描述

B 君有两个好朋友，他们叫宁宁和冉冉。有一天，冉冉遇到了一个有趣的题目：输入 b;d;n，求

输入

一行三个整数 b;d;n

输出

一行一个数表示模 7528443412579576937 之后的结果。

样例输入

1 5 9

样例输出

76

提示

其中 0<b^2<=d<(b+1)^2<=10^18,n<=10^18，并且 b mod 2=1,d mod 4=1

---

题解

数论 高中数学

注意题目中给出的0<b^2<=d<(b+1)^2，这说明了什么？

就是在变相的告诉我们b<=√d<b+1，也就是-1<b-√d<=0，即0<=|b-√d|<1。

那么0<=|b-√d|^n<1，可以看出这个数对整数部分的影响是常数级的。

不妨设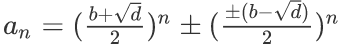

那么an一定恒为整数。

将n=1代入，可知两个±号一定相同，于是只有2种情况

再由通项公式求递推公式，发现只有一种情况符合条件，即：

，通项公式为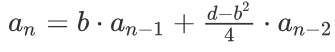

根据题目条件b mod 2=1,d mod 4=1可知前面的系数都为整数，于是可以矩阵乘法来推。

推完之后再讨论后一项的影响即可。

ps: n可能等于0，所以需要特判或者从a0开始推。

ps2: 题目中mod较大，需要用到unsigned long long和快速乘

#include <cstdio>
#include <cstring>
#include <algorithm>
#define mod 7528443412579576937ull
using namespace std;
typedef unsigned long long ull;
ull qmul(ull x , ull y)
{
    ull ans = 0;
    while(y)
    {
        if(y & 1) ans = (ans + x) % mod;
        x = (x + x) % mod;
        y >>= 1;
    }
    return ans;
}
struct matrix
{
    int n , m;
    ull num[2][2];
    matrix()
    {
        n = m = 0 , memset(num , 0 , sizeof(num));
    }
    matrix operator*(matrix a)
    {
        matrix t;
        t.n = n , t.m = a.m;
        int i , j , k;
        for(i = 0 ; i < t.n ; i ++ )
            for(j = 0 ; j < t.m ; j ++ )
                for(k = 0 ; k < m ; k ++ )
                    t.num[i][j] = (t.num[i][j] + qmul(num[i][k] , a.num[k][j])) % mod;
        return t;
    }
}A , B;
matrix qpow(matrix x , ull y)
{
    matrix t;
    t.n = x.n , t.m = x.m;
    int i;
    for(i = 0 ; i < x.n ; i ++ )
        t.num[i][i] = 1;
    while(y)
    {
        if(y & 1) t = t * x;
        x = x * x;
        y >>= 1;
    }
    return t;
}
int main()
{
    ull b , d , n , x , y , ans;
    scanf("%llu%llu%llu" , &b , &d , &n);
    x = b , y = (d - b * b) / 4;
    A.n = 1 , A.m = 2 , A.num[0][0] = 2 , A.num[0][1] = b;
    B.n = 2 , B.m = 2 , B.num[0][1] = y , B.num[1][0] = 1 , B.num[1][1] = x;
    ans = (A * qpow(B , n)).num[0][0];
    if(y && n % 2 == 0) ans = (ans + mod - 1) % mod;
    printf("%llu\n" , ans);
    return 0;
}