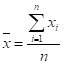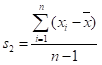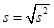day-12 python实现简单线性回归和多元线性回归算法
1、问题引入
在统计学中,线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。一个带有一个自变量的线性回归方程代表一条直线。我们需要对线性回归结果进行统计分析。
例如,假设我们已知一些学生年纪和游戏时间的数据,可以建立一个回归方程,输入一个新的年纪时,预测该学生的游戏时间。自变量为学生年纪,因变量为游戏时间。当只有一个因变量时,我们称该类问题为简单线性回归。当游戏时间与学生年纪和学生性别有关,因变量有多个时,我们称该类问题为多元线性回归。
2、常见的统计量
在研究该问题之前,首先了解下编程中用到的常见的统计量:
|
序号 |
概念 |
公式 |
算法 |
说明 |
|
1 |
均值 |
|
整体的均值 |
|
|
2 |
中位数 |
排序后取中间值 |
||
|
3 |
众数 |
出现次数最多的数 |
出现频率 |
|
|
4 |
方差 |
|
数据的离散程度 |
|
|
5 |
标准差 |
|
s |
方差的开方 |
2、简单线性回归实例及编程实现
研究一个自变量(X)和一个因变量(y)的关系
简单线性回归模型定义:

简单线性回归方程:
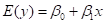
其中:
 为回归线的截距
为回归线的截距
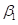 为回归线的斜率
为回归线的斜率
通过训练数据,求取出估计参数建立的直线方程:
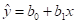
实际编程时,主要是根据已知训练数据,估计出 和
和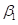 的值
的值 和
和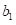
以下面实例为例,第一列表示每月投放广告的次数,第二列表示汽车向量,通过Python编程求取线性回归方程:
|
投放广告数 |
汽车销量 |
|
1 |
14 |
|
3 |
24 |
|
2 |
18 |
|
1 |
17 |
|
3 |
27 |
编程关键在于如何求取b0和b1的值,我们引入一个方程(sum of square):
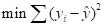
当上述方程的值最小时,我们认为求取到线程回归方程参数的值,对该方程求最小值可以进一步转化为求导和求极值的问题,求导过程省略,最后结论如下:
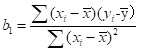
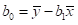
实际代码:
import numpy as np
from matplotlib import pylab as pl # 定义训练数据
x = np.array([1,3,2,1,3])
y = np.array([14,24,18,17,27]) # 回归方程求取函数
def fit(x,y):
if len(x) != len(y):
return
numerator = 0.0
denominator = 0.0
x_mean = np.mean(x)
y_mean = np.mean(y)
for i in range(len(x)):
numerator += (x[i]-x_mean)*(y[i]-y_mean)
denominator += np.square((x[i]-x_mean))
print('numerator:',numerator,'denominator:',denominator)
b0 = numerator/denominator
b1 = y_mean - b0*x_mean
return b0,b1 # 定义预测函数
def predit(x,b0,b1):
return b0*x + b1 # 求取回归方程
b0,b1 = fit(x,y)
print('Line is:y = %2.0fx + %2.0f'%(b0,b1)) # 预测
x_test = np.array([0.5,1.5,2.5,3,4])
y_test = np.zeros((1,len(x_test)))
for i in range(len(x_test)):
y_test[0][i] = predit(x_test[i],b0,b1) # 绘制图像
xx = np.linspace(0, 5)
yy = b0*xx + b1
pl.plot(xx,yy,'k-')
pl.scatter(x,y,cmap=pl.cm.Paired)
pl.scatter(x_test,y_test[0],cmap=pl.cm.Paired)
pl.show()
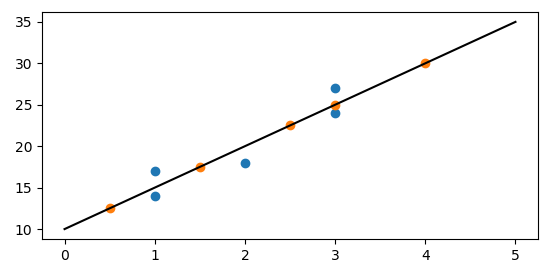
蓝色表示测试数据,橙色表示预测数据。
3、多元线性回归实例及编程实现
多元线性回归方程和简单线性回归方程类似,不同的是由于因变量个数的增加,求取参数的个数也相应增加,推导和求取过程也不一样。
y=β0+β1x1+β2x2+ ... +βpxp+ε
对于b0、b1、…、bn的推导和求取过程,引用一个第三方库进行计算。以如下数据为例,对运输里程、运输次数与运输总时间的关系,建立多元线性回归模型:
|
运输里程 |
运输次数 |
运输总时间 |
|
100 |
4 |
9.3 |
|
50 |
3 |
4.8 |
|
100 |
4 |
8.9 |
|
100 |
2 |
6.5 |
|
50 |
2 |
4.2 |
|
80 |
2 |
6.2 |
|
75 |
3 |
7.4 |
|
65 |
4 |
6.0 |
|
90 |
3 |
7.6 |
|
90 |
2 |
6.1 |
代码如下:
import numpy as np
from sklearn import datasets,linear_model # 定义训练数据
x = np.array([[100,4,9.3],[50,3,4.8],[100,4,8.9],
[100,2,6.5],[50,2,4.2],[80,2,6.2],
[75,3,7.4],[65,4,6],[90,3,7.6],[90,2,6.1]])
print(x)
X = x[:,:-1]
Y = x[:,-1]
print(X,Y) # 训练数据
regr = linear_model.LinearRegression()
regr.fit(X,Y)
print('coefficients(b1,b2...):',regr.coef_)
print('intercept(b0):',regr.intercept_) # 预测
x_test = np.array([[102,6],[100,4]])
y_test = regr.predict(x_test)
print(y_test)
如果特征向量中存在分类型变量,例如车型,我们需要进行特殊处理:
|
运输里程 |
输出次数 |
车型 |
隐式转换 |
运输总时间 |
|
100 |
4 |
1 |
010 |
9.3 |
|
50 |
3 |
0 |
100 |
4.8 |
|
100 |
4 |
1 |
010 |
8.9 |
|
100 |
2 |
2 |
001 |
6.5 |
|
50 |
2 |
2 |
001 |
4.2 |
|
80 |
2 |
1 |
010 |
6.2 |
|
75 |
3 |
1 |
010 |
7.4 |
|
65 |
4 |
0 |
100 |
6.0 |
|
90 |
3 |
0 |
100 |
7.6 |
|
100 |
4 |
1 |
010 |
9.3 |
|
50 |
3 |
0 |
100 |
4.8 |
|
100 |
4 |
1 |
010 |
8.9 |
|
100 |
2 |
2 |
001 |
6.5 |
import numpy as np
from sklearn.feature_extraction import DictVectorizer
from sklearn import linear_model # 定义数据集
x = np.array([[100,4,1,9.3],[50,3,0,4.8],[100,4,1,8.9],
[100,2,2,6.5],[50,2,2,4.2],[80,2,1,6.2],
[75,3,1,7.4],[65,4,0,6],[90,3,0,7.6],
[100,4,1,9.3],[50,3,0,4.8],[100,4,1,8.9],[100,2,2,6.5]])
x_trans = []
for i in range(len(x)):
x_trans.append({'x1':str(x[i][2])})
vec = DictVectorizer()
dummyX = vec.fit_transform(x_trans).toarray()
x = np.concatenate((x[:,:-2],dummyX[:,:],x[:,-1].reshape(len(x),1)),axis=1)
x = x.astype(float)
X = x[:,:-1]
Y = x[:,-1]
print(x,X,Y) # 训练数据
regr = linear_model.LinearRegression()
regr.fit(X,Y)
print('coefficients(b1,b2...):',regr.coef_)
print('intercept(b0):',regr.intercept_)
day-12 python实现简单线性回归和多元线性回归算法的更多相关文章
- python实现简单线性回归
之前推导了一元线性回归和多元线性回归,今天就用python来实现一下一元线性回归 先看下之前推导的结果 , 第一种是用循环迭代的计算方法.这里的x,y是numpy中的array类型 def su ...
- R语言解读多元线性回归模型
转载:http://blog.fens.me/r-multi-linear-regression/ 前言 本文接上一篇R语言解读一元线性回归模型.在许多生活和工作的实际问题中,影响因变量的因素可能不止 ...
- 斯坦福机器学习视频笔记 Week2 多元线性回归 Linear Regression with Multiple Variables
相比于week1中讨论的单变量的线性回归,多元线性回归更具有一般性,应用范围也更大,更贴近实际. Multiple Features 上面就是接上次的例子,将房价预测问题进行扩充,添加多个特征(fea ...
- TensorFlow从0到1之TensorFlow实现多元线性回归(16)
在 TensorFlow 实现简单线性回归的基础上,可通过在权重和占位符的声明中稍作修改来对相同的数据进行多元线性回归. 在多元线性回归的情况下,由于每个特征具有不同的值范围,归一化变得至关重要.这里 ...
- TensorFlow多元线性回归实现
多元线性回归的具体实现 导入需要的所有软件包: 因为各特征的数据范围不同,需要归一化特征数据.为此定义一个归一化函数.另外,这里添加一个额外的固定输入值将权重和偏置结合起来.为此定义函数 appe ...
- python语言和R语言实现机器学习算法
<转>机器学习系列(9)_机器学习算法一览(附Python和R代码) 转自http://blog.csdn.net/han_xiaoyang/article/details/51191 ...
- 梯度下降法的python代码实现(多元线性回归)
梯度下降法的python代码实现(多元线性回归最小化损失函数) 1.梯度下降法主要用来最小化损失函数,是一种比较常用的最优化方法,其具体包含了以下两种不同的方式:批量梯度下降法(沿着梯度变化最快的方向 ...
- 多元线性回归----Java简单实现
http://www.cnblogs.com/wzm-xu/p/4062266.html 多元线性回归----Java简单实现 学习Andrew N.g的机器学习课程之后的简单实现. 课程地址:h ...
- 多元线性回归(Multivariate Linear Regression)简单应用
警告:本文为小白入门学习笔记 数据集: http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearnin ...
随机推荐
- 11java基础继承
一. 继承相关 18.实现如下类之间的继承关系,并编写Music类来测试这些类. package com.hry.test; public class Instrument { ...
- JVM构架、GC垃圾回收机制的理解
JVM是Java Virtual Machine(Java虚拟机)的缩写 1.程序计数器 它的作用可以看做是当前线程所执行的字节码的行号指示器. 每个线程都有一个程序计算器,就是一个指针,指向方法区 ...
- mysql的子查询in()操作及按指定顺序显示
代码示例: in(逗号分隔开的值列表) 释:是否存在于值列表中 --------------------- 示例: select * from test where id in(3,1,5) orde ...
- js使用hover事件做一个“个人中心”的浮动层
原材料知识点:hover html: css:
- rest_framework -- 认证组件
#####认证组件##### 一.认证是什么就不说了,某些网页必须是用户登陆之后,才能访问的,所以这时候就需要用上认证组件. 你不用rest_framework的认证组件也行,这种认证的话,完全可以自 ...
- Django url处理
Django如何处理一个请求当一个用户请求Django 站点的一个页面,下面是Django 系统决定执行哪个Python 代码遵循的算法:1:Django 决定要使用的根URLconf 模块.通常,这 ...
- Kali 配置ssh服务器
SSH服务器配置 ssh是大多数Linux大佬必备的一样东西.Linux在工作中通常是命令行界面为主,那么就必定会使用ssh进行远程登录.下面我们介绍ssh配置和使用. 操作系统:kali-linux ...
- java程序执行系统命令
String cmd="orakill orcl 1233";//解锁数据库表 Process proc = Runtime.getRuntime().exec(cmd);
- ko绑定----记录
1.绑定变量 globalData = ko.observable({item:{}}); 2.绑定html ko.applyBindings(globalData, document.getElem ...
- hive-show-partitions
展示分区命令 show partitions show partitions 可以展示这个表格之下的所有分区信息.这个命令常常用在使用SQL语句操作数据之前.举个简单的例子,如果我们想要根据uid融合 ...