数论Keynote

【同余】

1、整数a，b对模m同余的充分与必要条件是m|(a-b)，即a=b+mt，t是整数。

2、性质丁。若a1=b1(mod m)，a2=b2(mod m)，则(a1+a2)=(b1+b2)(mod m)。

　  推论，a+b=c(mod m)，-b=-b(mod m)，则a=c-b(mod m)。

3、性质戊。若a1=b1(mod m)，a2=b2(mod m)，则a1a2=b1b2(mod m)。

　  推论，ak=bk(mod m)。特别地当k=d时，a/d=b/d(mod m)。

　　

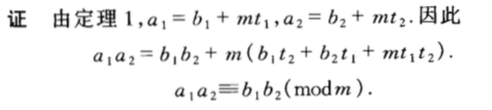
　　2）和 3）可得一个推论，若a＝b（mod m），对任意意常量k1,k2，ak1+k2=bk1+k2(mod m)。

4、性质己。若a1d=b1d(mod m)，且(d,m)=1，则a1=b1。

　　

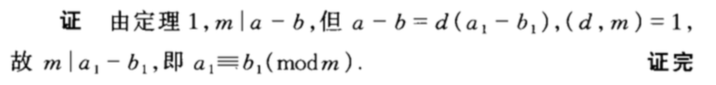
　　利用了定理："12、若(a,c)=1，c|ab，则c|b。"

5、性质壬。若a=b(mod m)，d|m，d>0，则 a=b(mod d)。

6、若a，b mod m同余，则(a,m)=(b,m)，因为a=b+mt，即a、b，b、m的因数相同。

7、m是一个正整数，则全部整数可分成m个集合，记作K0，K1，...Km-1。其中Kr是由一切形如qm+r的整数。K0,K1，...Km-1叫做m的剩余类，若a1...am个数均在不同的剩余类，则a1...am叫做m的一个完全剩余系。

8、m个数组成完全剩余系的充要条件是两两对m不同余。

9、欧拉函数：o(a)表示 0~(a-1)中与a互质的数的个数。

10、与M素质的剩余类中各取一数，组成的集合叫简化剩余系。简化剩余系成员的个数就是欧拉函数。

11、若（a,m）=1，x通过m的简化剩余系，则ax通过m的简化剩余系。

　　

12、若m1,m2互质，则o(m1m2)=o(m1)o(m2)，o()表示欧拉函数。

13、若p是质数，则o(p^a)=p^a-p^(a-1)。

　　

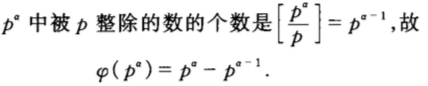
14、若 a = p^a1*p^a2*.. *pk^ak。是o(a) = a(1-1/p1)(1-1/p2).. (1- 1/pk)。

　　

15、m1、m2是互质的两个正整数，x1、x2分别通过模m1、m2的完全剩余系，则m2x1+m1x2通过模m1m2的完全剩余系。

用反证法可轻易证明。

【不定方程】

1、二元一次不定方程：ax+by=c，若其中一解为(x0,y0)，设(a,b)=d，a=a1*d,b=b1*d。则二元一次不定方程的一切解可以表示为：

　　x=x0-b1t，y=y0+a1t。t=0,+/-1,+/-2...

2、二元一次不定方程：ax+by=c，有解的充要条件是(a,b)|c。

3、根据定理a[(-1)^)(n-1)Qn]+b[(-1)n*Pn]=1，可以得出二元一次不定方程的其中一组解x=(-1)^(n-1)Qn,y=(-1)^n*Pn。

4、不定方程：x^2+y^2=z^2 的一切正整数解中以用下列以式表出来：

　　x=2ab，y=a^2-b^2, z=a^2+b^2。

【关键定理】

1、a = bq +c，则（a,b）= (b,c)。此为欧几里德法。

2、若c|ab，且(a,c)=1，则c|b。

3、a,b是任意两个不全为零的数，则存在两个数s,t，使得：as+bt=(a,b)

4、整数a，b对模m同余的充分与必要条件是m|(a-b)，即a=b+mt，t是整数。

5、性质丁。若a1=b1(mod m)，a2=b2(mod m)，则(a1+a2)=(b1+b2)(mod m)。

6、性质戊。若a1=b1(mod m)，a2=b2(mod m)，则a1a2=b1b2(mod m)。

7、性质己。若a1d=b1d(mod m)，且(d,m)=1，则a1=b1。

8、若（a,m）=1，x通过m的简化剩余系，则ax通过m的简化剩余系。通过反证法很容易证明。