ACM-线段树
http://blog.csdn.net/libin56842/article/details/8530197
基础可以看上面这篇文章
风格:
maxn是题目给的最大区间,而节点数要开4倍,确切的说……
lson和rson辨别表示结点的左孩子和右孩子。
PushUp(int rt)是把当前结点的信息更新到父节点
PushDown(int rt)是把当前结点的信息更新给孩子结点。
rt表示当前子树的根(root),也就是当前所在的结点。
思想:
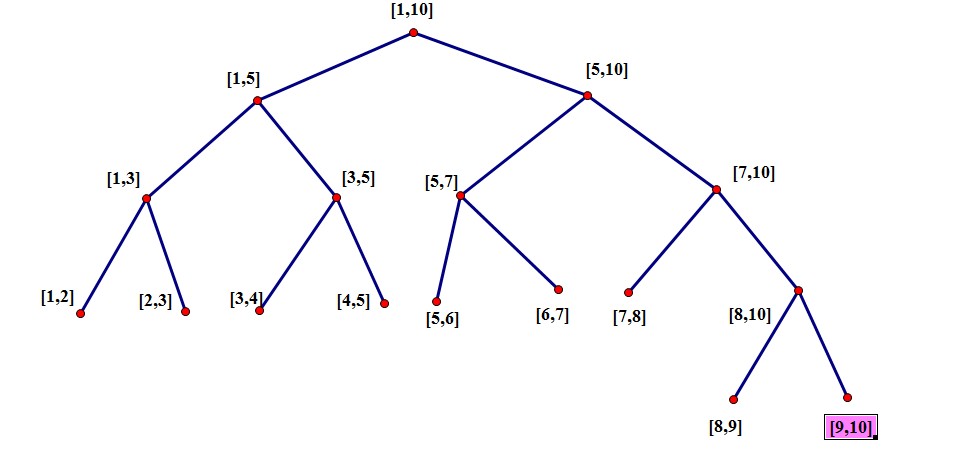
对于每个非叶节点所标示的结点 [a,b],其做孩子表示的区间是[a,(a+b)/2],其右孩子表示[(a+b)/2,b].
构造:
离散化和线段树:
题目:x轴上有若干个线段,求线段覆盖的总长度。
普通解法:设置坐标范围[min,max],初始化为0,然后每一段分别染色为1,最后统计1的个数,适用于线段数目少,区间范围小。
离散化的解法:离散化就是一一映射的关系,即将一个大坐标和小坐标进行一一映射,适用于线段数目少,区间范围大。
例如:[10000,22000],[30300,55000],[44000,60000],[55000,60000].
第一步:排序 10000 22000 30300 44000 55000 60000
第二部:编号 1 2 3 4 5 6
第三部:用编号来代替原数,即小数代大数 。
[10000,22000]~[1,2]
[30300,55000]~[3,5]
[44000,60000]~[4,6]
[55000,60000]~[5,6]
然后再用小数进行普通解法的步骤,最后代换回去。
线段树的解法:线段树通过建立线段,将原来染色O(n)的复杂度减小到 log(n),适用于线段数目多,区间范围小的情况。
离散化的线段树:适用于线段数目多,区间范围大的情况。
构造:
动态数据结构:
struct node{
node* left;
node* right;
……
}
静态全局数组模拟(完全二叉树):
struct node{
int left;
int right;
……
}Tree[MAXN]
http://www.xuebuyuan.com/1470670.html
线段树主要用四种用法
单点更新:
模板:
单点增减,查询线段和
struct node
{
int l,r,c;
}T[MAXN*]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int l,int x)
{
if(T[x].l == T[x].r && T[x].l == l)
{
T[x].c += val;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
update(val,l,(x<<) + );
}
else
{
update(val,l,x<<);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans += T[x].c;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
}
HDU 1166
#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <cctype>
#include <vector>
#include <iterator>
#include <set>
#include <map>
#include <sstream>
using namespace std; #define mem(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define spf sprintf
#define pb push_back
#define debug printf("!\n")
#define MAXN 55555
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define pqueue priority_queue
#define INF 0x3f3f3f3f struct node
{
int l,r,c;
}T[MAXN*]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int l,int x)
{
if(T[x].l == T[x].r && T[x].l == l)
{
T[x].c += val;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
update(val,l,(x<<) + );
}
else
{
update(val,l,x<<);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans += T[x].c;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
} int main()
{
int t,i,kase=;
char d[];
sf("%d",&t);
while(t--)
{
mem(T,);
pf("Case %d:\n",kase++);
sf("%d",&n);
build(,n,);
for(i=;i<=n;i++)
{
int tmp;
sf("%d",&tmp);
update(tmp,i,);
} while (sf("%s",d) != EOF)
{
if (d[] == 'E') break;
int x, y;
sf("%d%d", &x, &y);
if (d[] == 'Q')
{
ans = ;
query(x,y,);
pf("%d\n",ans);
}
if (d[] == 'S') update(-y,x,);
if (d[] == 'A') update(y,x,);
}
}
return ;
}
单点替换,查询线段最高
模板:
struct node
{
int l,r,c;
}T[MAXN*]; void PushUp(int rt)
{
T[rt].c = max(T[rt<<].c,T[(rt<<)+].c);
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int l,int x)
{
if(T[x].l == T[x].r && T[x].l == l)
{
T[x].c = val;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
update(val,l,(x<<) + );
}
else
{
update(val,l,x<<);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans = max(ans,T[x].c);
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
}
hdu 1754
这边要注意,输入字符不要用%c,会导致一些难以预料的问题
#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <cctype>
#include <vector>
#include <iterator>
#include <set>
#include <map>
#include <sstream>
using namespace std; #define mem(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define spf sprintf
#define pb push_back
#define debug printf("!\n")
#define MAXN 200005
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define pqueue priority_queue
#define INF 0x3f3f3f3f struct node
{
int l,r,c;
}T[MAXN*]; void PushUp(int rt)
{
T[rt].c = max(T[rt<<].c,T[(rt<<)+].c);
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int l,int x)
{
if(T[x].l == T[x].r && T[x].l == l)
{
T[x].c = val;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
update(val,l,(x<<) + );
}
else
{
update(val,l,x<<);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans = max(ans,T[x].c);
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
} int main()
{
int t,i,kase=;
while(sf("%d%d",&n,&m)==)
{
build(,n,);
for(i=;i<=n;i++)
{
int tmp;
sf("%d",&tmp);
update(tmp,i,);
}
while (m--)
{
int x,y;
char d[]; sf("%s %d %d",d,&x, &y);
//pf("%s %d %d\n",d,x,y);
if (d[] == 'Q')
{
ans = ;
query(x,y,);
pf("%d\n",ans);
}
if (d[] == 'U') update(y,x,);
}
}
return ;
}
成段更新
(通常这对初学者来说是一道坎),需要用到延迟标记(或者说懒惰标记),简单来说就是每次更新的时候不要更新到底,用延迟标记使得更新延迟到下次需要更新or询问到的时候
http://blog.sina.com.cn/s/blog_a2dce6b30101l8bi.html
区间替换,求总和
数组要开4倍才够
第一种思路,标记
模板:
struct node
{
int l,r,c,f;
}T[MAXN<<2]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
//pf("%d %d\n",rt,T[rt].c);
} void PushDown(int rt,int m)
{
if(T[rt].f)
{
T[rt<<].f = T[(rt<<) + ].f = T[rt].f;
T[rt<<].c = T[rt].f * (m-(m>>));
T[(rt<<)+].c = T[rt].f * (m>>);
T[rt].f = ;
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
T[x].f = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
PushUp(x);
} void update(int val,int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
T[x].f = val;
T[x].c = val*(r-l+);
//pf("%d %d %d\n",T[x].c,l,r);
return;
}
PushDown(x,r-l+);
//pf("%d %d %d %d %d %d\n",val,L,R,l,r,x); int mid = (l + r)>>;
if (L <= mid)
{
update(val,L,R,l,mid,x<<);
}
if(R > mid)
{
update(val,L,R,mid+,r,x<<|);
}
PushUp(x);
}
第二种思路,杂色
struct node
{
int l,r,c;
}T[MAXN<<]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
} void PushDown(int rt)
{
if(T[rt].c != -)//如果该区间只有一种颜色
{
T[rt<<].c = T[rt<<|].c = T[rt].c;//由于后面必定对子树操作,所以更新子树的值等于父亲的值
T[rt].c = -;//由于该区域颜色与修改不同,而且不是给定区域,所以该区域必定为杂色
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int L,int R,int x)
{
if(T[x].c == val) return;//相同则不用修改了
if(T[x].l == L && T[x].r == R)//找到了区间,直接更新
{
T[x].c = val;
return;
}
PushDown(x); //父区间为杂色时对所有子节点进行操作
int mid = (T[x].l + T[x].r)>>;
if(L>mid)
update(val,L,R,x<<|);
else if(R<=mid)
update(val,L,R,x<<);
else
{
update(val,L,mid,x<<);
update(val,mid+,R,x<<|);
}
}
hdu 1698
http://www.tuicool.com/articles/j6N3eaz
这里链接的其实不对,要求总和,所以每个点不能初始化为1
#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <cctype>
#include <vector>
#include <iterator>
#include <set>
#include <map>
#include <sstream>
using namespace std; #define mem(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define spf sprintf
#define pb push_back
#define debug printf("!\n")
#define MAXN 100000 + 5
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define pqueue priority_queue
#define INF 0x3f3f3f3f struct node
{
int l,r,c,f;
}T[MAXN<<2]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
//pf("%d %d\n",rt,T[rt].c);
} void PushDown(int rt,int m)
{
if(T[rt].f)
{
T[rt<<].f = T[(rt<<) + ].f = T[rt].f;
T[rt<<].c = T[rt].f * (m-(m>>));
T[(rt<<)+].c = T[rt].f * (m>>);
T[rt].f = ;
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].c = ;
T[x].f = ;
if (l == r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
PushUp(x);
} void update(int val,int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
T[x].f = val;
T[x].c = val*(r-l+);
//pf("%d %d %d\n",T[x].c,l,r);
return;
}
PushDown(x,r-l+);
//pf("%d %d %d %d %d %d\n",val,L,R,l,r,x); int mid = (l + r)>>;
if (L <= mid)
{
update(val,L,R,l,mid,x<<);
}
if(R > mid)
{
update(val,L,R,mid+,r,x<<|);
}
PushUp(x);
} int n,m,ans; void query(int l,int r,int x)
{
if(T[x].l == l && T[x].r == r)
{
ans += T[x].c;
return;
}
int mid = (T[x].l + T[x].r)>>;
if (l > mid)
{
query(l,r,(x<<)+);
}
else if(r<=mid)
{
query(l,r,(x<<));
}
else
{
query(l,mid,(x<<));
query(mid+,r,(x<<)+);
}
} int a[MAXN]; int main()
{
int t,i,kase=;
sf("%d",&t);
while(t--)
{
sf("%d",&n);
build(,n,);
sf("%d",&m);
for(i=;i<=m;i++)
{
int x,y,z;
sf("%d%d%d",&x,&y,&z);
update(z,x,y,,n,);
}
pf("Case %d: The total value of the hook is %d.\n",kase++,T[].c);
}
return ;
}
区间增减,区间求和
模板:
struct node
{
LL l,r,c,f;
}T[MAXN<<]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
//pf("%d %d\n",rt,T[rt].c);
} void PushDown(int rt,int m)
{
if(T[rt].f)
{
T[rt<<].f += T[rt].f;
T[(rt<<) + ].f += T[rt].f;
T[rt<<].c += T[rt].f * (m-(m>>));
T[(rt<<)+].c += T[rt].f * (m>>);
T[rt].f = ;
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].f = ;
T[x].c = ;
if(l==r) return;
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
} void update(int val,int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
T[x].f += val;
T[x].c += val*(r-l+);
//pf("%d %d %d\n",T[x].c,l,r);
return;
}
PushDown(x,r-l+);
//pf("%d %d %d %d %d %d\n",val,L,R,l,r,x); int mid = (l + r)>>;
if (L <= mid)
{
update(val,L,R,l,mid,x<<);
}
if(R > mid)
{
update(val,L,R,mid+,r,x<<|);
}
PushUp(x);
} LL ans; int n,m; void query(int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
ans += T[x].c;
return;
}
PushDown(x,r-l+);
int mid = (l + r)>>;
if(L <= mid) query(L,R,l,mid,x<<);
if(R > mid) query(L,R,mid+,r,x<<|);
PushUp(x);
}
poj 3468
#include <iostream>
#include <string>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <stack>
#include <queue>
#include <cctype>
#include <vector>
#include <iterator>
#include <set>
#include <map>
#include <sstream>
using namespace std; #define mem(a,b) memset(a,b,sizeof(a))
#define pf printf
#define sf scanf
#define spf sprintf
#define pb push_back
#define debug printf("!\n")
#define MAXN 111111 + 5
#define MAX(a,b) a>b?a:b
#define blank pf("\n")
#define LL long long
#define ALL(x) x.begin(),x.end()
#define INS(x) inserter(x,x.begin())
#define pqueue priority_queue
#define INF 0x3f3f3f3f struct node
{
LL l,r,c,f;
}T[MAXN<<]; void PushUp(int rt)
{
T[rt].c = T[rt<<].c + T[(rt<<)+].c;
//pf("%d %d\n",rt,T[rt].c);
} void PushDown(int rt,int m)
{
if(T[rt].f)
{
T[rt<<].f += T[rt].f;
T[(rt<<) + ].f += T[rt].f;
T[rt<<].c += T[rt].f * (m-(m>>));
T[(rt<<)+].c += T[rt].f * (m>>);
T[rt].f = ;
}
} void build(int l,int r,int x)
{
T[x].l = l;
T[x].r = r;
T[x].f = ;
if(l==r)
{
scanf("%I64d",&T[x].c);
return;
}
int mid = (l+r)>>;
build(l,mid,x<<);
build(mid+,r,(x<<) + );
PushUp(x);
} void update(int val,int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
T[x].f += val;
T[x].c += val*(r-l+);
//pf("%d %d %d\n",T[x].c,l,r);
return;
}
PushDown(x,r-l+);
//pf("%d %d %d %d %d %d\n",val,L,R,l,r,x); int mid = (l + r)>>;
if (L <= mid)
{
update(val,L,R,l,mid,x<<);
}
if(R > mid)
{
update(val,L,R,mid+,r,x<<|);
}
PushUp(x);
} LL ans; int n,m; void query(int L,int R,int l,int r,int x)
{
if(L <= l && r <= R)
{
ans += T[x].c;
return;
}
PushDown(x,r-l+);
int mid = (l + r)>>;
if(L <= mid) query(L,R,l,mid,x<<);
if(R > mid) query(L,R,mid+,r,x<<|);
} int main()
{
int t,i,kase=;
while(~sf("%d%d",&n,&m))
{
build(,n,);
/*
for(i=1;i<=n;i++)
{
int tmp;
sf("%d",&tmp);
update(tmp,i,i,1,n,1);
}
*/
for(i=;i<=m;i++)
{
int x,y,z;
char s[];
sf("%s",s);
if(s[]=='Q')
{
ans = ;
sf("%d%d",&x,&y);
query(x,y,,n,);
pf("%I64d\n",ans);
}
else
{
sf("%d%d%d",&x,&y,&z);
update(z,x,y,,n,);
}
}
}
return ;
}
ACM-线段树的更多相关文章
- hdu acm 1166 敌兵布阵 (线段树)
敌兵布阵 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submi ...
- 【ACM】hud1166 敌兵布阵(线段树)
经验: cout 特别慢 如果要求速度 全部用 printf !!! 在学习线段树 内容来自:http://www.cnblogs.com/shuaiwhu/archive/2012/04/22/24 ...
- ACM: Billboard 解题报告-线段树
Billboard Time Limit:8000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Descript ...
- HDU 4911 http://acm.hdu.edu.cn/showproblem.php?pid=4911(线段树求逆序对)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4911 解题报告: 给出一个长度为n的序列,然后给出一个k,要你求最多做k次相邻的数字交换后,逆序数最少 ...
- HDU 5029 Relief grain(离线+线段树+启发式合并)(2014 ACM/ICPC Asia Regional Guangzhou Online)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5029 Problem Description The soil is cracking up beca ...
- HDU 4031 Attack(离线+线段树)(The 36th ACM/ICPC Asia Regional Chengdu Site —— Online Contest)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4031 Problem Description Today is the 10th Annual of ...
- UPC 2224 Boring Counting ★(山东省第四届ACM程序设计竞赛 tag:线段树)
[题意]给定一个长度为N的数列,M个询问区间[L,R]内大于等于A小于等于B的数的个数. [题目链接]http://acm.upc.edu.cn/problem.php?id=2224 省赛的时候脑抽 ...
- 【线段树】HDU 5493 Queue (2015 ACM/ICPC Asia Regional Hefei Online)
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=5493 题目大意: N个人,每个人有一个唯一的高度h,还有一个排名r,表示它前面或后面比它高的人的个数 ...
- 2018牛客网暑假ACM多校训练赛(第七场)I Tree Subset Diameter 动态规划 长链剖分 线段树
原文链接https://www.cnblogs.com/zhouzhendong/p/NowCoder-2018-Summer-Round7-I.html 题目传送门 - https://www.n ...
- 2018牛客网暑假ACM多校训练赛(第六场)I Team Rocket 线段树
原文链接https://www.cnblogs.com/zhouzhendong/p/NowCoder-2018-Summer-Round6-I.html 题目传送门 - https://www.no ...
随机推荐
- Django 错误:TypeError at / 'bool' object is not callable
使用 Django自带的 auth 用户验证功能,编写函数,使用 is_authenticated 检查用户是否登录,结果报错: TypeError at / 'bool' object is not ...
- Java面向对象之内部类(访问格式)
一.基础概念 1.内部类是定义在类中的类.A类需要直接访问B类中的成员时,可以将A类定义到B类中,作为B类的内部类存在. 2.内部类可以相当于外部类中的一个成员,可以被成员修饰符所修饰.(如:publ ...
- [Swift实际操作]九、完整实例-(1)在iTunesConnect网站中创建产品
本文将通过一个实例项目,演示移动应用开发的所有步骤.首先要做的是打开浏览器,并进入[iTunesConnect网站],需要通过它创建一款自己的应用. 在iTunesConnect的登录页面中,输入自己 ...
- kill 进程的一些小细节
终止前台进程,可以用Ctrl+C组合键.但对于后台进程需要用kill命令. kill PID 还可以加信号(参数),默认情况下是编号为15的信号.term信号将终止所有不能捕捉该信号的进程. -s 可 ...
- 有关unixODBC:Data source name not found, and no default driver specified的问题
还是昨天测试postgresql的有关Mirroring Controller的功能时出的问题(真TM是个坑). 首先说下环境: 操作系统平台:RHEL6 x86_64 unixODBC版本:2.3. ...
- Puppet全面详解
1. 概述 puppet是一个开源的软件自动化配置和部署工具,它使用简单且功能强大,正得到了越来越多地关注,现在很多大型IT公司均在使用puppet对集群中的软件进行管理和部署,如google利用p ...
- js自定义对象 (转)
原文地址:https://sjolzy.cn/js-custom-object.html 29 March 2010 9:53 Monday by 小屋 javascript进阶之对象篇 一,概述 在 ...
- 洛谷 P1111 修复公路(最小生成树)
嗯... 题目链接:https://www.luogu.org/problemnew/show/P1111 这道题的关键是读懂题: 首先根据题中的一些扎眼的字眼我们可以判断这是一道用最小生成树来做的题 ...
- hdu3068 最长回文 马拉车模板题
题目传送门 马拉车算法模板题. 学习博客 #include<bits/stdc++.h> #define clr(a,b) memset(a,b,sizeof(a)) using name ...
- CDN基本原理和功能浅析
CDN的全称是Content Delivery Network,即内容分发网络.CDN的通俗理解就是网站加速,CPU均衡负载,可以解决跨运营商,跨地区,服务器负载能力过低,带宽过少等带来的网站打开速度 ...
