OJP1147括号匹配加强版(栈)与P1153乱头发节(单调栈)
惨兮兮的被刷掉2%的通过率后在经过思考和dalao的指点后终于A掉了这道题
强烈建议修改这题的样例,实在太迷惑人,各种错误算法都能过
比如说这是一份错误代码,看懂了也不要学思路,和正解不知道差到哪里去了:

惨兮兮,WA掉代码:
#include <iostream>
#include <iomanip>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <ctime>
using namespace std;
char a[100086];
int len,top=0,ll=0,lexn,maxx=-10000,leen;
char s[100086],bb[10086],jg[100086];
bool f=true;
int main()
{
memset(a,0,sizeof(a));
memset(s,0,sizeof(s));
cin>>a;
len=strlen(a);
for(int i=0;i<len;i++)
{
if(s[top]=='(')
{
if(a[i]==']')
{memset(s,0,sizeof(s));memset(bb,0,sizeof(bb));top=0;f=false;}
else if(a[i]=='(')
{
s[++top]=a[i];
bb[++ll]=a[i];
}
else if(a[i]==')')
{
bb[++ll]=a[i];
top--;
}
}
else if(s[top]=='[')
{
if(a[i]==')')
{memset(s,0,sizeof(s));memset(bb,0,sizeof(bb));top=0;f=false;}
else if(a[i]=='(')
{
s[++top]=a[i];
bb[++ll]=a[i];
}
else if(a[i]==']')
{
bb[++ll]=a[i];
top--;
}
}
else if(a[i]=='('||a[i]=='[')
{s[++top]=a[i];bb[++ll]=a[i];}
if(top==0&&f)
{
//lexn=strlen(bb);
if(maxx<ll)
{
memset(jg,0,sizeof(jg));
maxx=ll;
if(leen!=maxx)
leen=0;
for(int i=1;i<=ll;i++)
{
jg[i]=bb[i];
leen++;
}
}
ll=0;
memset(bb,0,sizeof(bb));
memset(s,0,sizeof(s));
}
if(!f)
f=true;
}
for(int i=1;i<=leen;i++)
{
if(jg[i]=='['||jg[i]=='('||jg[i]==']'||jg[i]==')')
cout<<jg[i];
}
return 0;
}(这是WA掉的)
但即便是这个WA掉所有数据的错误代码都能过样例,所以改一下为好吧……
然后是正解思路:
读入一个char型数组,然后将此数组中的字符挨个进栈,如果栈顶为’]’或是’)’,查看第top-1个元素,如果是能与当前字符匹配的左括号,就出栈,bool型数组标记下标,否则就将栈清空,然而操作还是讲不清,代码如下:
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <algorithm>
using namespace std;
int len,s=0,maxx=-1000,top=-1,sum=-1,num=-1,t=0;//top为栈顶下标,因为是字符串,所以为-1,sum,num同理
char a[1000086],stack[1000086];
bool f[1000086];
int d[1000010],e[1000010];//开两个数组分别记录'('和']'的下标
int main()
{
cin>>a;
memset(f,false,sizeof(f));
len=strlen(a);
for(int i=0;i<len;i++)
{
stack[++top]=a[i];//入栈
if(stack[top]=='(')//当栈顶是(时,记录下标
d[++sum]=i;
if(stack[top]=='[')//同上
e[++num]=i;
if((stack[top]==')'&&stack[top-1]=='[')||(stack[top]==']'&&stack[top-1]=='('))//当右括号与栈顶左括号不匹配时,栈清空
top=0;
else if((stack[top]==')'&&stack[top-1]=='(')||(stack[top]==']'&&stack[top-1]=='['))//当栈顶左括号与右括号匹配时
{
f[i]=1;//标记当前下标
if(stack[top]==']')//如果栈顶右括号为]?
{
f[e[num]]=1;//bool数组标记下标
num--;//存储]的数组减去一个]
}
if(stack[top]==')')//理同上
{
f[d[sum]]=1;
sum--;
}
top-=2;//因为左括号与右括号匹配,所以直接删去两个
}
}
for(int i=0;i<len;i++)
{
if(f[i])//t为能够匹配的括号式的长度
t++;
else//因为匹配括号式必须挨着,所以一旦!f[i],则说明已经记录完了一个括号式
{
if(t>maxx)//标记最大长度
{
maxx=t;
s=i;//s记录当前下标
}
t=0;
}
}
if(t>maxx)//避免式子在最后
{
maxx=t;
s=len;
}
for(int i=s-maxx;i<s;i++)//s减去maxx即为最长表达式的起始下标
cout<<a[i];
return 0;
}

作为我校校本教材题目…教育价值大于题目价值系列
单调栈,就是具有单调性的栈,单调递增或是单调递减。
以上面那道奶牛题距离,最基本最暴力的解法就是二重循环枚举统计,但是N(1<=N<=80,000)的范围二重枚举肯定会超,所以显然暴力枚举是不行了。但是我们如果仔细思考一下就会发现,对于符合条件的情况来看,牛的高度是单调的,一旦h[i+1]>=h[i],就不符合条件了。采用逆向思维,对于第i头牛来说,如果它是第一个比第k头牛高的,那么第k头牛能看到的牛的距离就是i-k-1头(不要问我为什么要减一,第k头牛看不到自己的头)。
比如6头牛,高度分别是:10,3,7,4,12,2。第5头牛高度12,那么第4头就被第5头的高度维护掉了,第三头就只能看到1头,第一头能看到三头,而第二头被第三头的高度维护掉了。我们要做的是用栈维护牛与牛之间单调递减的局部关系。
1) 如果当前元素大于栈顶元素,栈顶出栈,统计栈顶看见了几头牛。
2) 如果栈为空,或当前元素比栈顶小,当前元素进栈。
因为操作只有当前元素进一次栈出一次栈,所以复杂度是O(n)。
代码如下:
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <ctime>
#include <cmath>
using namespace std;
const int maxx=1000090;
int stack[maxx],a[maxx],top=0,n,t;
long long gg=0;//gg为统计的奶牛能看到的头数.
inline void push(int x)//进栈
{stack[++top]=x;}
inline int pop()//出栈
{return stack[top--];}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
push(1);
for(int i=2;i<=n;i++)
{
while((a[stack[top]]<=a[i])&&(top>0))
{
t=pop();
gg+=i-t-1;
}
push(i);
}
while(top>0)//处理最高的那个奶牛,若最高的奶牛不是最后一头,就要解决最高的那头所看到的奶牛数。
{
t=pop();
gg+=n-t;
}
cout<<gg<<endl;
return 0;
}
然后还有另一个思路,但是因为我校评测机的问题,不能A掉,但实际输出与测试数据是符合的,很迷,比较尬的是,我校校本教材上给出的这个思路的代码不仅会CE,而且程序连样例的过不去,WA声一片,所以进行了修改。其思路在于,先读入第一个元素,然后按照正常的方式向后找,注意:for循环为for(int i=1;i<n;i++),但如果有比第一个元素还大的高度,就将栈清空,将当前元素入栈,再进行搜索,而且很重要的是,top的大小就是在这一时刻此前所有的能看到当前奶牛的总和,例如:6 5 3 2 8。比如第3头牛高度为3,前两头都能看见,此时top=2,则ans+=top就是ans+=2。第4头牛前三头都能看到,top=3,ans+=top就是ans+=3。
代码如下:
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstring>
#include <ctime>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxx=100000;
int s[maxx],m,n,top=0;
long long ans=0,f=1;
inline void push(int m)
{s[++top]=m;}
inline int pop()
{return s[top--];}
int main()
{
cin>>n;
cin>>m;
push(m);
for(int i=1;i<n;i++)
{
cin>>m;
if((s[top]<=m)&&(top>0))
{
pop();
if(s[1]<=m)//如果有比栈中第一个元素要大的,将栈清空,当前元素继续向下搜索
f=0;
}
if(f==0)//接上
{top=0;}
else
ans+=top;//top的大小就是之前的牛能看到的牛的总和
push(m);
f=1;
}
cout<<ans<<endl;
return 0;
}
然后大概到这里,栈得学习就结束了系列
OJP1147括号匹配加强版(栈)与P1153乱头发节(单调栈)的更多相关文章
- jzyzoj 栈——P1148:括号匹配加强版
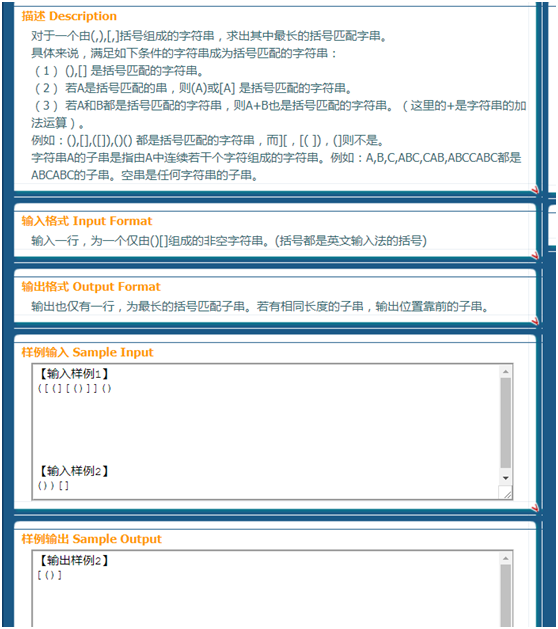
括号匹配加强版 描述 Description 对于一个由(,),[,]括号组成的字符串,求出其中最长的括号匹配字串. 具体来说,满足如下条件的字符串成为括号匹配的字符串: (1) (),[] 是括号匹 ...
- bzoj1660:[Usaco2006 Nov]badhair乱头发节
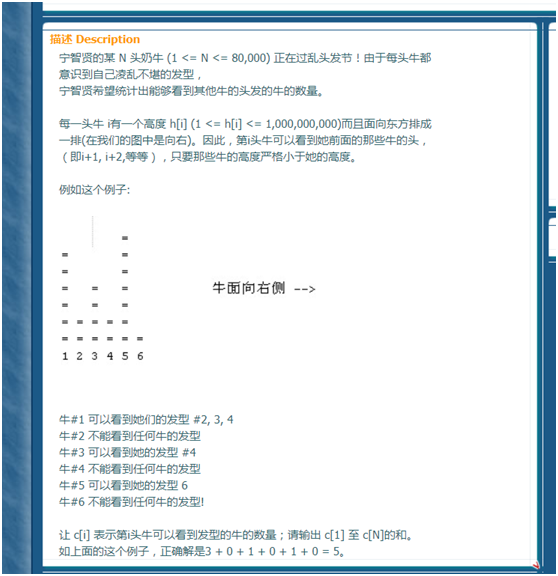
Description 农民John的某 N 头奶牛 (1 <= N <= 80,000) 正在过乱头发节!由于每头牛都 意识到自己凌乱不堪的发型, FJ 希望统计出能够看到其他牛的头发的 ...
- JZOJ 1264. 乱头发节
1264. 乱头发节(badhair.pas/c/cpp) (File IO): input:badhair.in output:badhair.out Time Limits: 1000 ms M ...
- BZOJ1660: [Usaco2006 Nov]Bad Hair Day 乱发节(单调栈)
题意 题目链接 Sol 单调栈板子题.. 找到向左第一个比他大的位置,然后判断一下就可以了 #include<bits/stdc++.h> //#define int long long ...
- BZOJ 1660: [Usaco2006 Nov]Bad Hair Day 乱发节( 单调栈 )
维护一个h严格递减的栈 , 出栈时计算一下就好了.. ------------------------------------------------------------------------- ...
- 括号匹配(C++ Stack)
最近在学习C++,所以使用stack容器来实现括号匹配 /**********************************************************/ stack<Ty ...
- 洛谷P2866 [USACO06NOV]糟糕的一天Bad Hair Day(单调栈)
题目描述 Some of Farmer John's N cows (1 ≤ N ≤ 80,000) are having a bad hair day! Since each cow is self ...
- [USACO06NOV]糟糕的一天Bad Hair Day BZOJ 1660 单调栈
农民John的某 N 头奶牛 (1 <= N <= 80,000) 正在过乱头发节!由于每头牛都 意识到自己凌乱不堪的发型, FJ 希望统计出能够看到其他牛的头发的牛的数量. 每一头牛 i ...
- 【DP/单调栈】关于单调栈的一些题目(codevs 1159,codevs 2673)
CODEVS 2673:Special Judge 题目描述 Description 这个月的pku月赛某陈没有参加,因为当时学校在考试[某陈经常逃课,但某陈还没有强大到考试也可以逃掉的程度].何 ...
随机推荐
- Netscaler的超高端口复用助力应对公网地址紧张
Netscaler的超高端口复用助力应对公网地址紧张 http://blog.51cto.com/caojin/1898351 经常会有人问一个IP只有65535(姑且不考虑预留端口),从Big-ip ...
- 【心情】HNOI2018游记
Day 0. 全机房的人好像都在做题.然而下午是社团节的游园会,身为社干的我风风雨雨在外面各种搬凳子搬椅子换场地招待外校同学……就这样我好像什么都没有复习. 晚上就一起去酒店了.大概因为是高一的缘故, ...
- [Leetcode] climbing stairs 爬楼梯
You are climbing a stair case. It takes n steps to reach to the top. Each time you can either climb ...
- 【BZOJ 3123】 [Sdoi2013]森林 主席树启发式合并
我们直接按父子关系建主席树,然后记录倍增方便以后求LCA,同时用并查集维护根节点,而且还要记录根节点对应的size,用来对其启发式合并,然后每当我们合并的时候我们都要暴力拆小的一部分重复以上部分,总时 ...
- HDU - 1880 魔咒词典~哈希入门
哈利波特在魔法学校的必修课之一就是学习魔咒.据说魔法世界有100000种不同的魔咒,哈利很难全部记住,但是为了对抗强敌,他必须在危急时刻能够调用任何一个需要的魔咒,所以他需要你的帮助. 给你一部魔咒词 ...
- HDU 多校对抗赛第二场 1010 Swaps and Inversions
Swaps and Inversions Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Oth ...
- Notepad++64插件安装方法
首先通过https://github.com/bruderstein/nppPluginManager/releases下载"nppPluginManager",下载解压后放到对应 ...
- 【NOIP1999】邮票面值设计 dfs+dp
题目传送门 这道题其实就是找一波上界比较麻烦 用一波 背包可以推出上界mx 所以新加入的物品价值一旦大于mx+1,显然就会出现断层,所以可以以maxm+1为枚举上界,然后这样进行下一层的dfs. 这样 ...
- Logistic函数
Logistic函数(又称sigmoid函数) Logistic函数或Logistic曲线是一种常见的S形函数,它是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关系 ...
- Linux ssh的使用
1.查看SSH客户端版本 有的时候需要确认一下SSH客户端及其相应的版本号.使用ssh -V命令可以得到版本号.需要注意的是,Linux一般自带的是OpenSSH: 下面的例子即表明该系统正在使用Op ...
