洛谷 P2827 蚯蚓 解题报告

P2827 蚯蚓

题目描述

本题中，我们将用符号 \(\lfloor c \rfloor\) 表示对 \(c\) 向下取整，例如：\(\lfloor 3.0 \rfloor = \lfloor 3.1 \rfloor = \lfloor 3.9 \rfloor = 3\)。

蛐蛐国最近蚯蚓成灾了！隔壁跳蚤国的跳蚤也拿蚯蚓们没办法，蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。

蛐蛐国里现在共有 \(n\) 只蚯蚓（\(n\) 为正整数）。每只蚯蚓拥有长度，我们设第 \(i\) 只蚯蚓的长度为 \(a_i\)(\(i=1,2,\dots,n\))，并保证所有的长度都是非负整数（即：可能存在长度为 \(0\) 的蚯蚓）。

每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只（如有多个则任选一个）将其切成两半。神刀手切开蚯蚓的位置由常数 \(p\)（是满足 \(0 < p < 1\) 的有理数）决定，设这只蚯蚓长度为 \(x\)，神刀手会将其切成两只长度分别为 \(\lfloor px \rfloor\) 和 \(x - \lfloor px \rfloor\) 的蚯蚓。特殊地，如果这两个数的其中一个等于 \(0\)，则这个长度为 \(0\) 的蚯蚓也会被保留。此外，除了刚刚产生的两只新蚯蚓，其余蚯蚓的长度都会增加 \(q\)（是一个非负整常数）。

蛐蛐国王知道这样不是长久之计，因为蚯蚓不仅会越来越多，还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是救兵还需要 \(m\) 秒才能到来……（\(m\) 为非负整数）

蛐蛐国王希望知道这 \(m\) 秒内的战况。具体来说，他希望知道：

\(m\) 秒内，每一秒被切断的蚯蚓被切断前的长度（有 \(m\) 个数）；

\(m\) 秒后，所有蚯蚓的长度（有 \(n + m\) 个数）。

蛐蛐国王当然知道怎么做啦！但是他想考考你……

输入输出格式

输入格式：

第一行包含六个整数 \(n,m,q,u,v,t\)，其中：\(n,m,q\) 的意义见【问题描述】；\(u,v,t\) 均为正整数；你需要自己计算 \(p=u / v\)（保证 \(0 < u < v\)）；\(t\) 是输出参数，其含义将会在【输出格式】中解释。

第二行包含 nn 个非负整数，为 \(a_1, a_2, \dots, a_n\)，即初始时 \(n\) 只蚯蚓的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。

保证 \(1 \leq n \leq 10^5\)，\(0 \leq m \leq 7 \times 10^6\)，\(0 < u < v \leq 10^9\)，\(0 \leq q \leq 200\)，\(1 \leq t \leq 71\)，\(0 \leq a_i \leq 10^8\)。

输出格式：

第一行输出 \(\left \lfloor \frac{m}{t} \right \rfloor\)个整数，按时间顺序，依次输出第 \(t\) 秒，第 \(2t\) 秒，第 \(3t\) 秒，……被切断蚯蚓（在被切断前）的长度。

第二行输出 \(\left \lfloor \frac{n+m}{t} \right \rfloor\)个整数，输出 \(m\) 秒后蚯蚓的长度；需要按从大到小的顺序，依次输出排名第 \(t\)，第 \(2t\)，第 \(3t\)，……的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。即使某一行没有任何数需要输出，你也应输出一个空行。

请阅读样例来更好地理解这个格式。

说明：

---

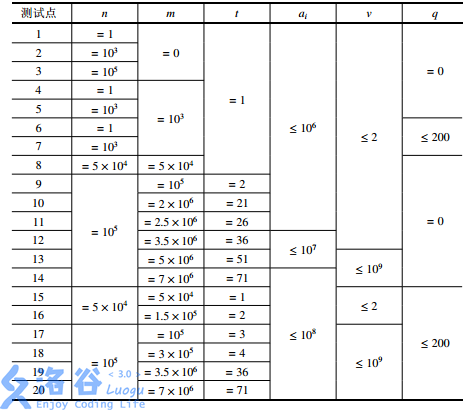
堆的做法很显然，大概有65~80pts，算是送了很多分了

一看输出都强行怕你T，那一定是\(O(n)\)了

记得合并果子有一个双队列\(O(n)\)做法吗？

事实上跟这个题差不多哒

我们开三个队列，一个存放原来的蚯蚓，一个存放被这样切\(\lfloor px \rfloor\)的蚯蚓，另一个存放被\(x - \lfloor px \rfloorx\)这样切的

注意到在后两个队列中先拿出来的一定比后拿出来的要长，具有单调性

对于第一个队列我们可以先排序，然后每次取三个队列中队尾最大的，切开放到相应的队头

增加的量我们可以维护一个被切断的时间点

注意中间过程可能会爆int

---

Code:

#include <cstdio>
#include <algorithm>
#define ll long long
const int N=8e6;
ll q1[N][2],q2[N][2],q3[N][2],l1=1,l2=1,l3=1,r1,r2,r3;
ll n,m,q,u,v,t,a[N];//n个m刀增q p=u/v t输出
int main()
{
    scanf("%lld%lld%lld%lld%lld%lld",&n,&m,&q,&u,&v,&t);
    for(int i=1;i<=n;++i)
        scanf("%lld",a+i);
    r1=n;
    std::sort(a+1,a+1+n);
    for(int i=1;i<=n;i++) q1[n+1-i][0]=a[i];
    for(register ll mx,id,i=1;i<=m;++i)
    {
        mx=0;
        if(l1<=r1&&mx<q1[l1][0]+(i-q1[l1][1]-1)*q) mx=q1[l1][0]+(i-q1[l1][1]-1)*q,id=1;
        if(l2<=r2&&mx<q2[l2][0]+(i-q2[l2][1]-1)*q) mx=q2[l2][0]+(i-q2[l2][1]-1)*q,id=2;
        if(l3<=r3&&mx<q3[l3][0]+(i-q3[l3][1]-1)*q) mx=q3[l3][0]+(i-q3[l3][1]-1)*q,id=3;
        if(i%t==0) printf("%lld ",mx);
        if(id==1) ++l1;if(id==2) ++l2;if(id==3) ++l3;
        q2[++r2][0]=mx*u/v,q2[r2][1]=i;
        q3[++r3][0]=mx-mx*u/v,q3[r3][1]=i;
    }
    printf("\n");ll i=0;
    while(l1<=r1||l2<=r2||l3<=r3)
    {
        ll id,mx=0;++i;
        if(l1<=r1&&mx<q1[l1][0]+(m-q1[l1][1])*q) mx=q1[l1][0]+(m-q1[l1][1])*q,id=1;
        if(l2<=r2&&mx<q2[l2][0]+(m-q2[l2][1])*q) mx=q2[l2][0]+(m-q2[l2][1])*q,id=2;
        if(l3<=r3&&mx<q3[l3][0]+(m-q3[l3][1])*q) mx=q3[l3][0]+(m-q3[l3][1])*q,id=3;
        if(i%t==0) printf("%lld ",mx);
        if(id==1) ++l1;if(id==2) ++l2;if(id==3) ++l3;
    }
    printf("\n");
    return 0;
}

---

2018.9.1