xgboost与gbdt区别

1.基分类器的选择：传统GBDT以CART作为基分类器，XGBoost还支持线性分类器，这个时候XGBoost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。

2.二阶泰勒展开：传统GBDT在优化时只用到一阶导数信息；XGBoost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶损失函数的导数。顺便提一下，XGBoost工具支持自定义损失函数，只要函数可一阶和二阶求导。GBDT和GBDT拟合的是都是残差。

　　a.二阶泰勒展开：

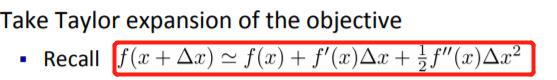
　　b.xgboost训练：

　　c.最后等式被优化成这个样子，包含gi和hi两个变量，因为ft(xi)是当前树的预测值，已知，而g_i和h_i是从损失函数来的，所以自定义的损失函数只要满足一阶和二阶可导就行，因为带入到整体的式子中要满足泰勒二阶展开。

3.方差-方差权衡：XGBoost在目标函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出分数的L2模的平方和。从Bias-variance tradeoff角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合，这也是XGBoost优于传统GBDT的一个特性。

4.Shrinkage（缩减）：相当于学习速率（xgboost中的）。XGBoost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。（补充：传统GBDT的实现也有学习速率）

5.列抽样（column subsampling）：XGBoost借鉴了随机森林的做法，支持列抽样，我们会在同一层的结点分割前先随机选一部分特征，遍历的时候只用遍历这部分特征就行了，不需要便利全部特征，不仅能降低过拟合，还能减少计算，这也是XGBoost异于传统GBDT的一个特性。

6.缺失值处理：XGBoost考虑了训练数据为稀疏值的情况，可以为缺失值或者指定的值指定分支的默认方向，这能大大提升算法的效率，论文中“枚举”指的不是枚举每个缺失样本在左边还是在右边，而是枚举缺失样本整体在左边，还是在右边两种情况。分裂点还是只评估特征不缺失的样本，paper提到50倍。即对于特征的值有缺失的样本，XGBoost可以自动学习出它的分裂方向。

7.XGBoost工具支持并行：

boosting不是一种串行的结构吗?怎么并行的？注意xgboost的并行不是tree粒度的并行，xgboost也是一次迭代完才能进行下一次迭代的（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。xgboost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），xgboost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。

8.线程缓冲区存储：按照特征列方式存储能优化寻找最佳的分割点，但是当以行计算梯度数据时会导致内存的不连续访问，严重时会导致cache miss，降低算法效率。paper中提到，可先将数据收集到线程内部的buffer（缓冲区），主要是结合多线程、数据压缩、分片的方法，然后再计算，提高算法的效率。

9.可并行的近似直方图算法：树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。大致的思想是根据百分位法列举几个可能成为分割点的候选者，然后从候选者中根据上面求分割点的公式计算找出最佳的分割点。