HDU 6057 Kanade's convolution

题目链接：HDU-6057

题意：

思路：先按照官方题解推导出下面的式子：

现在唯一的问题就是怎么解决[bit(x)-bit(y)=bit(k)]的问题。

我们定义\( F(A,k)_{i}=\left[ bit\left( i\right) =k\right] * A_{i} \)，相当于把A、B、C分别按照bit划分成m+1个序列。

有如下公式：

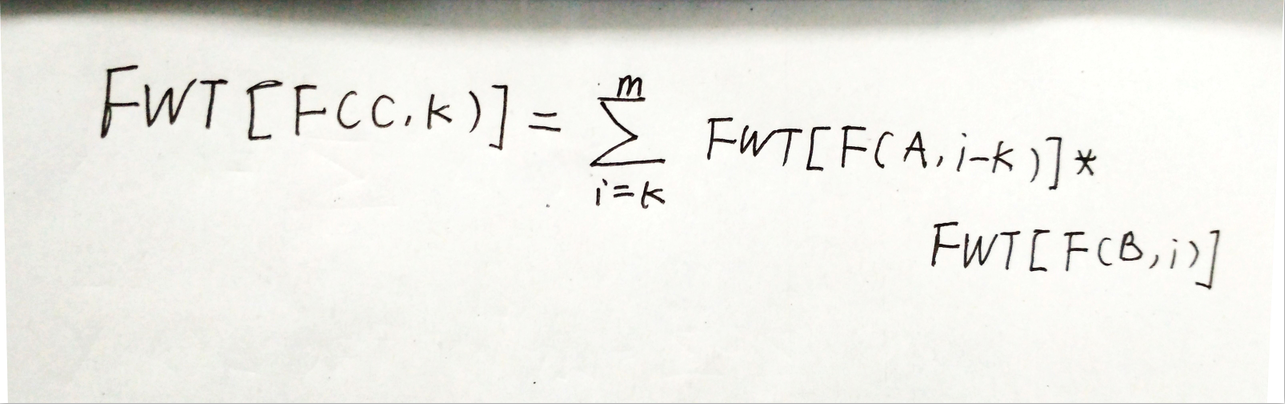
同时我们发现\( C_k=F(C,bit(k)))_k \)。

然后我们就可以搞出来啦！

代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 using namespace std;
 typedef long long LL;

 const LL MAXN=;
 const LL MOD=;
 LL A[][MAXN],B[][MAXN],C[][MAXN];
 LL two[];
 LL bit(LL x)
 {
     LL ret=;
     while(x>)
     {
         if(x&) ret++;
         x>>=;
     }
     return ret;
 }
 // 快速幂
 // 求x^n%mod
 // Verified!
 LL powMod(LL x,LL n,LL mod)
 {
     LL res=;
     while(n>)
     {
         if(n&) res=res*x % mod;
         x=x*x % mod;
         n>>=;
     }
     return res;
 }
 LL inv(LL a,LL m)
 {
     return powMod(a,m-,m);
     // return powMod(a,eularPhi(m)-1,m);
 }
 LL inv2;
 void FWT_Xor(LL *A, LL len) {
   if (len == ) return;
   LL len2 = len >> ;
   FWT_Xor(A, len2);
   FWT_Xor(A + len2, len2);
   for (LL i = ; i < len2; ++i) {
     LL x = A[i], y = A[i + len2];
     A[i] = (x + y) % MOD;
     A[i + len2] = ((((x - y) % MOD) + MOD) % MOD);
   }
 }
 void IFWT_Xor(LL *A, LL len) {
   if (len == ) return;
   LL len2 = len >> ;
   for (LL i = ; i < len2; ++i) {
     LL x = A[i], y = A[i + len2];
     A[i] = ((x + y) % MOD) * inv2 % MOD;
     A[i + len2] = ((((x - y) % MOD) + MOD) % MOD) * inv2 % MOD;
   }
   IFWT_Xor(A, len2);
   IFWT_Xor(A + len2, len2);
 }
 int main()
 {
 #ifdef LOCAL
     freopen("in.txt","r",stdin);
 #endif
     inv2=inv(,MOD);
     memset(A,,sizeof(A));
     memset(B,,sizeof(B));
     memset(C,,sizeof(C));
     two[]=;
     for(LL i=;i<;i++) two[i]=two[i-]*%MOD;

     LL m;
     scanf("%lld",&m);
     for(LL i=;i<(<<m);i++)
     {
         LL x;
         scanf("%lld",&x);
         A[bit(i)][i]=x*two[bit(i)]%MOD;
     }
     for(LL i=;i<(<<m);i++)
     {
         LL x;
         scanf("%lld",&x);
         B[bit(i)][i]=x;
     }
     for(LL i=;i<=m;i++) FWT_Xor(A[i],(<<m));
     for(LL i=;i<=m;i++) FWT_Xor(B[i],(<<m));
     for(LL k=;k<=m;k++)
         for(LL i=k;i<=m;i++)
             for(LL j=;j<(<<m);j++)
                 C[k][j]=(C[k][j]+A[i-k][j]*B[i][j])%MOD;
     for(LL i=;i<=m;i++) IFWT_Xor(C[i],(<<m));
     LL ans=,mi=;
     for(LL i=;i<(<<m);i++)
     {
         ans=(ans+C[bit(i)][i]*mi)%MOD;
         mi=mi*%MOD;
     }
     printf("%lld\n",ans);
     return ;
 }