MVVM模式View和ViewModel的通信

还需要些什么呢

在前面几篇博客中我们尝试去实现了MVVM中的数据绑定、命令绑定和事件绑定。貌似实现的差不多了。我最早尝试用MVVM去开发的时候也是这么想的，没有用第三方框架，甚至只是实现了数据绑定和命令绑定就开搞了，遇到需要订阅事件的时候就把代码写在后台。那时候经常自我洗脑：设计模式是死的，人是活的，不能犯教条主义错误，后台写点代码影响不大。我确实很好的贯彻了这个思想，逻辑自然是乱得一塌糊涂。后来认真学习了下，实现了事件绑定，感觉好了很多。但确走向了另一个极端，后台代码多写一行都会感觉很不爽。还有就是View和ViewModel的依赖，例如当需要在ViewModel中打开窗口，给窗口传值，在窗口关闭后获取返回值时，打开窗体的动作在ViewModel中进行吗？这样ViewModel又产生了对View的依赖了。还有当主窗体按下一个按钮，然后需要另外一个窗体做出响应的时候，窗体间要如何通信。当在ViewModel中使用其它线程影响到UI时怎么处理。这篇博客主要对这些问题简单说明一下。

View和ViewModel的通信

消息通信的方式主要受到MVVMLight的启发，MVVMLight实现了一套略有复杂的消息通信，包含了定类型发送、分组发送、发送给包含继承类型的目标、广播等。就目前我做的几个小项目来说，View和ViewModel通信本身用的就不是那么频繁，需求也不算旺盛，所以自己实现了一套比较简易的消息通信。View在实例化的时候注册消息，通过一个列表保存注册的消息，消息在发送的时候根据条件从列表中找到相应的消息并执行操作，如下图所示：

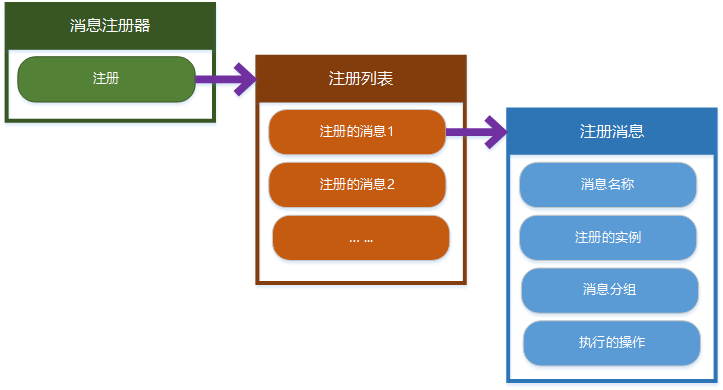
消息发送和处理：

比较奇怪的是为什么要引入一个消息注册器，在View的后台代码中直接注册不就可以了吗?好吧，其实最初的想法确实比较强迫症，只是单纯的不想在后台中写入太多的代码（我真不是处女座），这样看上去似乎更高端。不过后来想了下，View对ViewModel(虽然不是接口)和消息注册器实际上都算是一种依赖，而且View对ViewModel和消息注册器的依赖都是唯一的，也就是说一个View只有一个ViewModel和一个消息注册器。这样可以用控制反转的方式把对ViewModel和消息注册器的依赖一起注入进来，而且在注入过程中可以顺便配置ViewModel的Dispatcher以方便跨线程修改UI，也可以给ViewModel配置单独的MessageManager让View和ViewModel的通信进入另一个次元，不受其他消息干扰。这些在讨论ViewModel依赖注入的时候将会尝试。

关于跨线程修改UI

这个顺带提一下，因为实现起来很简单。在ViewModel中有时会遇到使用其它线程修改UI的情况，我之前是通过 App.Current.MainWindow.Dispatcher来获取UI线程的调度器的。当然也可以把UI线程的调度器保存到一个静态变量中以便随时访问。不过我一直没搞明白MaiWindow的Dispatcher和非MainWindow的Dispatcher有什么区别，不过还是在ViewModel的基类中加入了Dispatcher这个属性，这样在给View注入ViewModel的时候可以把ViewModel的Dispatcher设置为绑定的View的Dispatcher，虽然并不太清楚这有什么卵用 -_-|||