luoguP2123 皇后游戏——微扰法的应用与排序传递性的证明

题目背景

还记得 NOIP 2012 提高组 Day1 的国王游戏吗？时光飞逝，光阴荏苒，两年

过去了。国王游戏早已过时，如今已被皇后游戏取代，请你来解决类似于国王游

戏的另一个问题。

题目描述

皇后有 n 位大臣，每位大臣的左右手上面分别写上了一个正整数。恰逢国庆

节来临，皇后决定为 n 位大臣颁发奖金，其中第 i 位大臣所获得的奖金数目为第

i－1 位大臣所获得奖金数目与前 i 位大臣左手上的数的和的较大值再加上第 i 位

大臣右手上的数。

形式化地讲：我们设第 i 位大臣左手上的正整数为 ai，右手上的正整数为 bi，

则第 i 位大臣获得的奖金数目为 ci可以表达为：

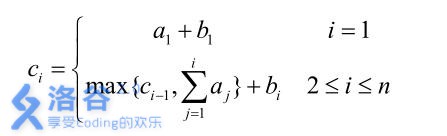
当然，吝啬的皇后并不希望太多的奖金被发给大臣，所以她想请你来重新安

排一下队伍的顺序，使得获得奖金最多的大臣，所获奖金数目尽可能的少。

注意：重新安排队伍并不意味着一定要打乱顺序，我们允许不改变任何一

位大臣的位置。

n<=20000，保证不会爆long long

题解：

参考/推荐：题解 P2123 【皇后游戏】

确实是一道值得深入思考的好问题！！！

背景既然提示了和国王游戏有关系，并且显然也是一个排序的贪心题目。

也一定是用微扰法（交换临项法）寻找并证明。

（因为交换相邻两项不会影响别的项）

不妨设，前面的一个人是i，后面一个人是i+1

i前面的一个人的c值为p,i前面的人的a总和是sum

那么，我们现在要找到i在i+1前面的条件。

①i在i+1前面：

贡献：

$max(max(p,sum+a_i)+b_i,sum+a_i+a_{i+1})+b_{i+1}$

化简一下就是：

$max(p+b_i+b_{i+1},sum+a_i+b_i+b_{i+1},sum+a_i+a_{i+1}+b_{i+1})$

②同理，i+1在i前面

化简以后是：

$max(p+b_i+b_{i+1},sum+a_{i+1}+b_i+b_{i+1},sum+a_i+a_{i+1}+b_i)$

我们现在要探究①小于②的条件

发现，共同有的是：$p+b_i+b_{i+1}$

这一项可以两边直接消掉。最终不会影响排序的结果。

那么就是比较：

$max(sum+a_i+b_i+b_{i+1},sum+a_i+a_{i+1}+b_{i+1})$

和

$max(sum+a_{i+1}+b_i+b_{i+1},sum+a_i+a_{i+1}+b_i)$

去掉sum，再化简一下：

$max(b_i,a_{i+1})+a_i+b_{i+1}<=max(b_{i+1},a_i)+a_{i+1}+b_i$

移项，

$max(b_i,a_{i+1})-a_{i+1}-b_i<=max(b_{i+1},a_i)-a_i-b_{i+1}$

其实这个式子的含义是：

两边的较大值会被减掉，较小值的相反数会留下来

所以，其实是：

$-min(a_{i+1},b_i)<=-min(a_i,b_{i+1})$

也就是：

$min(a_i,b_{i+1})<=min(a_{i+1},b_i)$

看似是一个很简单的公式！！

那么直接排序？

luogu反正是AC了。

但是其实不对！

我们发现，这个式子不具有传递性，

也就是说，

这种重载小于号的方式，并不满足

$a<=b,b<=c \space\ \to \space\ a<=c$

手动出几组就可以hack掉。

而我们的sort本质是快速排序实现的。

我们分治的每层子区间会选择一个随机的x作为基准，把小于x放在x左边，大于x放在x右边，

这个排序的正确性，显然要有<满足传递性的性质才行。

所以，这个式子用sort排出来，根据原始输入顺序、基准的x选取的不同，排出来的顺序也是不同的，答案也就是不同的了。

那么怎么办？

继续观察这个式子：

$min(a_i,b_{i+1})<=min(a_{i+1},b_i)$

可以（也许很难）想到，和ai，bi本身有关系？

显然，如果排序的式子和ai，bi本身放在一起，是一定有传递性的。

(例如：

$min(a_1,b_1)<=min(a_2,b_2),min(a_2,b_2)<=min(a_3,b_3) \space\ \to \space\ min(a_1,b_1)<=min(a_3,b_3)$

)

我们只好讨论了。

1.$a_i<b_i,a_{i+1}<b_{i+1}$

那么就是：$a_i<=a_{i+1}$

所以这一块按照a升序排序。

2.$a_i=b_i,a{i+1}=b_{i+1}$

随便排即可。

3.$a_i>b_i,a_{i+1}>b_{i+1}$

那么就是：$b_{i+1}<=b_i$

所以这一块按照b降序排序

那么，现在所有的序列会被分成这三大块。

块与块之间怎么办？

1应该在2前面。2应该在3前面。

即1前，2中，3后。

证明：

1在2前面，2在3前面显然可以证明。

设1、3中的一个元素分别是$(a_1,b_1),(a_3,b_3)$

因为有$a_1<b_1,a_3>b_3$

所以，一定有$min(a_1,b_3)<=min(a_3,b_1)$

 每个组内部有传递性，组与组之间也有传递性。

所以这种排序就具有传递性。

这样就可以了。

为了方便，可以定义一个人的组别d为：

$\frac{a_i-b_i}{|a_i-b_i|}$

1组对应-1，2组对应0，三组对应1

所以，我们的排序可以这样进行

先按照d为第一关键字，分到每个组里。

d相同，按照组内的排序方式。

（对了还有一个锅，重载的小于号不能带=，必须小于号才行。

因为快排的内部实现可能会出问题。

$while(a[i]<=a[x]) i++ $

i=x不会停止，假设x是最后一个，就可能数组越界！！ RE）

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=+;
int t,n;
struct node{
    int a,b;
    int d;
    bool friend operator <(node x,node y){
        if(x.d!=y.d) return x.d<y.d;
        if(x.d<=) return x.a<y.a;
        else return x.b>y.b;
    }
}a[N];
ll c[N];
int main(){
    scanf("%d",&t);
    while(t--){
        ll ans=;
        memset(c,,sizeof c);
        scanf("%d",&n);
        for(int i=;i<=n;i++)scanf("%d%d",&a[i].a,&a[i].b),a[i].d=(a[i].a-a[i].b)/abs(a[i].a-a[i].b);
        sort(a+,a+n+);
        ll sum=;
        for(int i=;i<=n;i++){
            sum+=a[i].a;
            c[i]=max(c[i-],sum)+a[i].b;
            ans=max(ans,c[i]);
        }
        printf("%lld\n",ans);
    }
    return ;
}

/*
   Author: *Miracle*
   Date: 2018/9/23 22:50:00
*/

总结：

非常非常非常非常....漂亮的一道题，不是算法的混杂，就是一个单单对排序的理解和处理。

大致的思路是：

1.微扰法思想，列式子。

2.化简式子。到了两个min的式子。

3.发现，不满足排序的传递性。

4.尽量向ai,bi本身的属性靠近，而不是加上相邻的项，把这个条件作为判定的条件（邻居毕竟不靠谱，可能是谁都不知道）

5.列出最终的式子。

6.证明了传递性的存在。

（根据快排的原理，然后注意重载小于号不能加=）

启示我们学习算法要学到算法的应用条件和原理本质上，

好比排序的<的定义要有传递性，快排不能<=会RE，微扰法本质的使用条件是，交换这两项，对前面后面的值都无影响。

而不是一知半解，囫囵吞枣，死记硬背，直接复制。

值得思考。

完结撒花~~~