Bresenham直线算法与画圆算法

在我们内部开发使用的一个工具中，我们需要几乎从 0 开始实现一个高效的二维图像渲染引擎。比较幸运的是，我们只需要画直线、圆以及矩形，其中比较复杂的是画直线和圆。画直线和圆已经有非常多的成熟的算法了，我们用的是Bresenham的算法。

计算机是如何画直线的？简单来说，如下图所示，真实的直线是连续的，但我们的计算机显示的精度有限，不可能真正显示连续的直线，于是我们用一系列离散化后的点（像素）来近似表现这条直线。

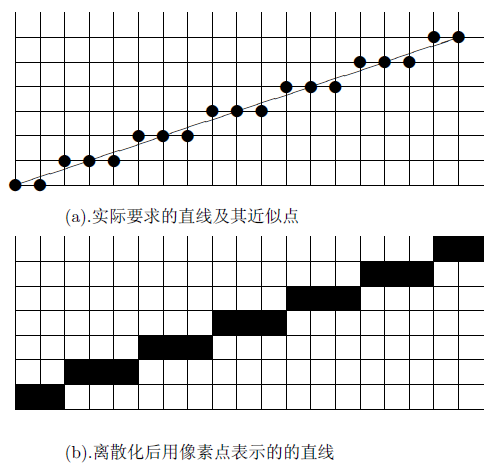
　　（上图来自于互联网络，《计算机图形学的概念与方法》柳朝阳，郑州大学数学系）

接下来的问题就是如何尽可能高效地找到这些离散的点，Bresenham直线算法就是一个非常不错的算法。

　　Bresenham直线算法是用来描绘由两点所决定的直线的算法，它会算出一条线段在 n 维光栅上最接近的点。这个算法只会用到较为快速的整数加法、减法和位元移位，常用于绘制电脑画面中的直线。是计算机图形学中最先发展出来的算法。

　　(引自wiki百科布雷森漢姆直線演算法)

这个算法的流程图如下：

可以看到，算法其实只考虑了斜率在 0 ~ 1 之间的直线，也就是与 x 轴夹角在 0 度到 45 度的直线。只要解决了这类直线的画法，其它角度的直线的绘制全部可以通过简单的坐标变换来实现。

下面是一个C语言实现版本。

// 交换整数 a 、b 的值
inline void swap_int(int *a, int *b) {
    *a ^= *b;
    *b ^= *a;
    *a ^= *b;
}

// Bresenham's line algorithm
void draw_line(IMAGE *img, int x1, int y1, int x2, int y2, unsigned long c) {
    // 参数 c 为颜色值
    int dx = abs(x2 - x1),
        dy = abs(y2 - y1),
        yy = ;

    if (dx < dy) {
        yy = ;
        swap_int(&x1, &y1);
        swap_int(&x2, &y2);
        swap_int(&dx, &dy);
    }

    int ix = (x2 - x1) >  ?  : -,
         iy = (y2 - y1) >  ?  : -,
         cx = x1,
         cy = y1,
         n2dy = dy * ,
         n2dydx = (dy - dx) * ,
         d = dy *  - dx;

    if (yy) { // 如果直线与 x 轴的夹角大于 45 度
        while (cx != x2) {
            if (d < ) {
                d += n2dy;
            } else {
                cy += iy;
                d += n2dydx;
            }
            putpixel(img, cy, cx, c);
            cx += ix;
        }
    } else { // 如果直线与 x 轴的夹角小于 45 度
        while (cx != x2) {
            if (d < ) {
                d += n2dy;
            } else {
                cy += iy;
                d += n2dydx;
            }
            putpixel(img, cx, cy, c);
            cx += ix;
        }
    }
}

可以看到，在画线的循环中，这个算法只用到了整数的加法，所以可以非常的高效。

接下来，我们再来看一看Bresenham画圆算法。

Bresenham画圆算法又称中点画圆算法，与Bresenham 直线算法一样，其基本的方法是利用判别变量来判断选择最近的像素点，判别变量的数值仅仅用一些加、减和移位运算就可以计算出来。为了简便起见，考虑一个圆 心在坐标原点的圆，而且只计算八分圆周上的点，其余圆周上的点利用对称性就可得到。

为什么只计算八分圆周上的点就可以了呢？和上面的直线算法类似，圆也有一个“八对称性”，如下图所示。

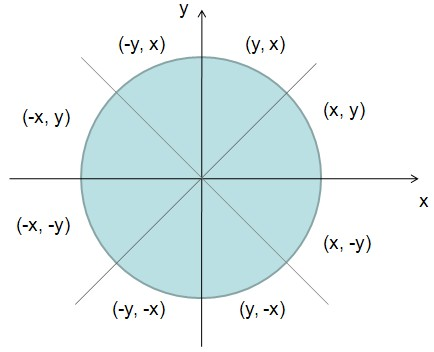
显然，我们只需要知道了圆上的一个点的坐标 (x, y) ，利用八对称性，我们马上就能得到另外七个对称点的坐标。

和直线算法类似，Bresenham画圆算法也是用一系列离散的点来近似描述一个圆，如下图。

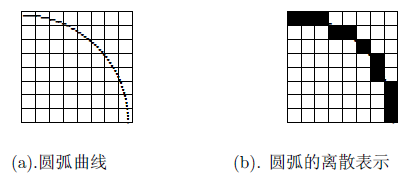
　　（上图来自于互联网络，《计算机图形学的概念与方法》柳朝阳，郑州大学数学系）

Bresenham画圆算法的流程图如下。

可以看到，与画线算法相比，画圆的循环中用到了整数的乘法，相对复杂了一些。

下面是一个C语言实现版本。

// 八对称性
inline void _draw_circle_8(IMAGE *img, int xc, int yc, int x, int y, unsigned long c) {
    // 参数 c 为颜色值
    putpixel(img, xc + x, yc + y, c);
    putpixel(img, xc - x, yc + y, c);
    putpixel(img, xc + x, yc - y, c);
    putpixel(img, xc - x, yc - y, c);
    putpixel(img, xc + y, yc + x, c);
    putpixel(img, xc - y, yc + x, c);
    putpixel(img, xc + y, yc - x, c);
    putpixel(img, xc - y, yc - x, c);
}

//Bresenham's circle algorithm
void draw_circle(IMAGE *img, int xc, int yc, int r, int fill, unsigned long c) {
    // (xc, yc) 为圆心，r 为半径
    // fill 为是否填充
    // c 为颜色值

    // 如果圆在图片可见区域外，直接退出
    if (xc + r <  || xc - r >= img->w ||
            yc + r <  || yc - r >= img->h) return;

    int x = , y = r, yi, d;
    d =  -  * r;

    if (fill) {
        // 如果填充（画实心圆）
        while (x <= y) {
            for (yi = x; yi <= y; yi ++)
                _draw_circle_8(img, xc, yc, x, yi, c);

            if (d < ) {
                d = d +  * x + ;
            } else {
                d = d +  * (x - y) + ;
                y --;
            }
            x++;
        }
    } else {
        // 如果不填充（画空心圆）
        while (x <= y) {
            _draw_circle_8(img, xc, yc, x, y, c);

            if (d < ) {
                d = d +  * x + ;
            } else {
                d = d +  * (x - y) + ;
                y --;
            }
            x ++;
        }
    }
}

 

可以看到，Bresenham画圆算法（中点圆算法）的实现也非常简单。在另一个项目中，我还有一个 Python 实现的版本，不过那段代码和其余部分结合得比较紧，有点难抠，这次就不贴出来了。