数据结构之Huffman树与最优二叉树

最近在翻炒一些关于树的知识，发现一个比较有意思的二叉树，huffman树，对应到离散数学中的一种名为最优二叉树的路径结构，而Huffman的主要作用，最终可以归结到一种名为huffman编码的编码方式，使用huffman编码方式，我们可以以平均长度最短的码字来记录一串信息，且每个信息分子的编码唯一，独立。从而最终合成编码所对应的信息唯一，无歧义。

huffman树的创建时基于每个信息分子都拥有其权重，权重越大，越靠近树根，即路径越短，

下面我们我们来以一个huffman树的例子为例：简单引入一下huffman树：

上图即是构造huffman编码所必备的元素，那么，通过上图中的信息分子与对应编码，我们就可以写出编码解析结果唯一且无歧义的编码串  如：

001011110100111     CDGFH

000111110010          CHEF

huffman编码的任何组合方式都只可能对应一串信息，不可能有歧义出现。 因为在huffman树中，每一个信息元都是一个叶子节点。。。

期huffman树形结果为：

圆圈中的数字表示权重，我们规定向左为0   向右为1 ，， 即的到上面表格中的huffman编码，通过上图中的树，我们不难算出树的权

W(T)为291651   必为所有的由这些信息元组合成的树中的权的最小值，当然，组合方式有可能不一样，但最终的权，只会大于或等于他，即不存在与权值相等且为最小权值的非同构的两颗树。

如何创建这个huffman树(最优二叉树)呢，这才是我们今天的关键。

首先我们需要明确一样东西，基于信息元所创建的huffman树的节点个数是否确定，答案是肯定的，如果在一开始我们所要创建的数据结构的长度是确定的话，那么我觉得我们有很大的必要选择数组了。

数组的长度：m = 信息元个数n * 2 - 1；   即我们需要n个单元存放信息元节点，n-1的单元来存放分支点(内点和根节点)。

数组单元的数据结构(不考虑信息元数据)：

由于树的存储结构是用数组实现的，故parent，rchild，lchild中直接保存数组下标即可。

一切都具备好了，那哥们儿几个就来初始化一下这棵树把(以上面的例子为例)：

(初始状态，还未进行建树):

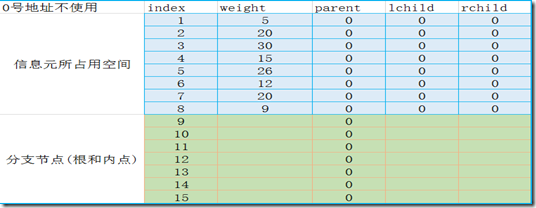
建树动作完成之后：

咦，中间的步骤哪里去了呢？？？   别急！！！

听我说：  1：寻找数组中单元数据的parent不为零的两个数组元c1 ， c2

2：找到他们的父节点father，父节点：数组index递增序列中第一个weight为零的数组元(前提：信息元中不存在weight为零的权)。

3：将父节点的lchild指向c1 和 c2中序号(index)在前面的那个数组单元(即lchild = indexMin(c1，c2).index)， rchild则等于另一个的index，将c1和c2的parent都指向找到的父节点，即c1/c2.parent = father.index。同时c1和c2的权之和赋给father的weight(权)

4：重复1,2,3，直到左右数组单元的weight都被数据化(赋值)。

代码如下：

void HuffmanCoding(HuffmanTree *HT,int *w,int n)
{  /*w为权值数组，n为信息元个数*/
   int m,i,s1,s2;
   HuffmanTree p;
   char *cd;
   if(n<=)
     return;
   m=*n-;
   *HT=(HuffmanTree)malloc((m+)*sizeof(HTNode)); /* 0号单元未用 */
   for(p=*HT+,i=;i<=n;++i,++p,++w)    //parent lcahid rchild全部初始化为零
   {
     (*p).weight=*w;
     (*p).parent=;
     (*p).lchild=;
     (*p).rchild=;
   }
   for(;i<=m;++i,++p)
     (*p).parent=;
   for(i=n+;i<=m;++i) /* 建赫夫曼树 */
   { /* 在HT[1~i-1]中选择parent为0且weight最小的两个结点,其序号分别为s1和s2 */
     select(*HT,i-,&s1,&s2);
     (*HT)[s1].parent=(*HT)[s2].parent=i;
     (*HT)[i].lchild=s1;
     (*HT)[i].rchild=s2;
     (*HT)[i].weight=(*HT)[s1].weight+(*HT)[s2].weight;
   }
}

那么，最终的huffman编码如何实现，以及我们如何起实现反编码(从编码得到信息)，笔者将会最今后的日子里进行探讨(没时间啦啦)，阿里亚瑟哦，觉得不错的话，记得点赞哦。