朴素贝叶斯算法 & 应用实例

转载请注明出处：http://www.cnblogs.com/marc01in/p/4775440.html

引

和师弟师妹聊天时经常提及，若有志于从事数据挖掘、机器学习方面的工作，在大学阶段就要把基础知识都带上。机器学习在大数据浪潮中逐渐展示她的魅力，其实《概率论》、《微积分》、《线性代数》、《运筹学》、《信息论》等几门课程算是前置课程，当然要转化为工程应用的话，编程技能也是需要的，而作为信息管理专业的同学，对于信息的理解、数据的敏感都是很好的加分项。

不过光说不练，给人的留下的印象是极为浅薄的，从一些大家都熟悉的角度切入，或许更容易能让人有所体会。

下面进入正题。

BTW,如果观点错误或者引用侵权的欢迎指正交流。

一、朴素贝叶斯算法介绍

朴素贝叶斯，之所以称为朴素，是因为其中引入了几个假设（不用担心，下文会提及）。而正因为这几个假设的引入，使得模型简单易理解，同时如果训练得当，往往能收获不错的分类效果，因此这个系列以naive bayes开头和大家见面。

因为朴素贝叶斯是贝叶斯决策理论的一部分，所以我们先快速了解一下贝叶斯决策理论。

假设有一个数据集，由两类组成（简化问题），对于每个样本的分类，我们都已经知晓。数据分布如下图（图取自MLiA）：

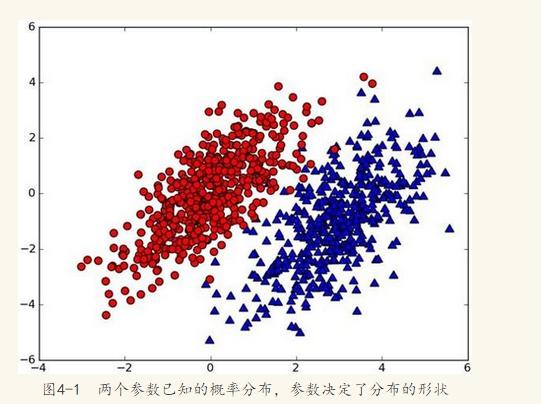
现在出现一个新的点new_point (x,y)，其分类未知。我们可以用p1(x,y)表示数据点(x,y)属于红色一类的概率，同时也可以用p2(x,y)表示数据点(x,y)属于蓝色一类的概率。那要把new_point归在红、蓝哪一类呢？

我们提出这样的规则：

如果p1(x,y) > p2(x,y)，则(x,y)为红色一类。

如果p1(x,y) <p2(x,y), 则(x,y)为蓝色一类。

换人类的语言来描述这一规则：选择概率高的一类作为新点的分类。这就是贝叶斯决策理论的核心思想，即选择具有最高概率的决策。

用条件概率的方式定义这一贝叶斯分类准则：

如果p(red|x,y) > p(blue|x,y), 则(x,y)属于红色一类。

如果p(red|x,y) < p(blue|x,y), 则(x,y)属于蓝色一类。

也就是说，在出现一个需要分类的新点时，我们只需要计算这个点的

max(p(c1 | x,y),p(c2 | x,y),p(c3 | x,y)...p(cn| x,y))。其对于的最大概率标签，就是这个新点的分类啦。

那么问题来了，对于分类i 如何求解p(ci| x,y)？

没错，就是贝叶斯公式：

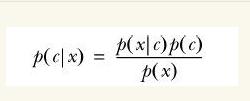
公式暂不推导，先描述这个转换的重要性。红色、蓝色分类是为了帮助理解，这里要换成多维度说法了，也就是第二部分的实例：判断一条微信朋友圈是不是广告。

前置条件是：我们已经拥有了一个平日广大用户的朋友圈内容库，这些朋友圈当中，如果真的是在做广告的，会被“热心网友”打上“广告”的标签，我们要做的是把所有内容分成一个一个词，每个词对应一个维度，构建一个高维度空间 (别担心，这里未出现向量计算)。

当出现一条新的朋友圈new_post，我们也将其分词，然后投放到朋友圈词库空间里。

这里的X表示多个特征（词）x1,x2,x3...组成的特征向量。

P(ad|x)表示：已知朋友圈内容而这条朋友圈是广告的概率。

利用贝叶斯公式，进行转换：

P(ad|X) = p(X|ad) p(ad) / p(X)

P(not-ad | X) = p(X|not-ad)p(not-ad) / p(X)

比较上面两个概率的大小，如果p(ad|X) > p(not-ad|X),则这条朋友圈被划分为广告，反之则不是广告。

看到这儿，实际问题已经转为数学公式了。

看公式推导 (公式图片引用):

朴素贝叶斯分类的正式定义如下：

1、设为一个待分类项，而每个a为x的一个特征属性。

2、有类别集合。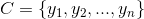

3、计算。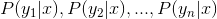

4、如果，则。

那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：

1、找到一个已知分类的待分类项集合，这个集合叫做训练样本集。

2、统计得到在各类别下各个特征属性的条件概率估计。即。

3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

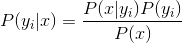
因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

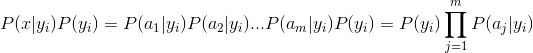
这里要引入朴素贝叶斯假设了。如果认为每个词都是独立的特征，那么朋友圈内容向量可以展开为分词(x1,x2,x3...xn)，因此有了下面的公式推导：

　　P(ad|X) = p(X|ad)p(ad) = p(x1, x2, x3, x4...xn | ad) p(ad)

假设所有词相互条件独立，则进一步拆分：

虽然现实中，一条朋友圈内容中，相互之间的词不会是相对独立的，因为我们的自然语言是讲究上下文的╮(╯▽╰)╭，不过这也是朴素贝叶斯的朴素所在，简单的看待问题。

至此，P(xi|ad)很容易求解，P(ad)为词库中广告朋友圈占所有朋友圈（训练集）的概率。我们的问题也就迎刃而解了。

二、构造一个文字广告过滤器。

到这里，应该已经有心急的读者掀桌而起了，捣鼓半天，没有应用。 (╯‵□′)╯︵┻━┻

"Talk is cheap, show me the code."

逻辑均在代码注释中，因为用python编写，和伪代码没啥两样，而且我也懒得画图……

 #encoding:UTF-8

 '''

 Author: marco lin

 Date: 2015-08-28

 '''

 from numpy import *

 import pickle

 import jieba

 import time

 stop_word = []

 '''

     停用词集, 包含“啊，吗，嗯”一类的无实意词汇以及标点符号

 '''

 def loadStopword():

     fr = open('stopword.txt', 'r')

     lines = fr.readlines()

     for line in lines:

         stop_word.append(line.strip().decode('utf-8'))

     fr.close()

 '''

     创建词集

     params:

         documentSet 为训练文档集

     return:词集, 作为词袋空间

 '''

 def createVocabList(documentSet):

     vocabSet = set([])

     for document in documentSet:

         vocabSet = vocabSet | set(document) #union of the two sets

     return list(vocabSet)

 '''

     载入数据

 '''

 def loadData():

     return None

 '''

    文本处理，如果是未处理文本，则先分词（jieba分词）,再去除停用词

 '''

 def textParse(bigString, load_from_file=True):    #input is big string, #output is word list

     if load_from_file:

         listOfWord = bigString.split('/ ')

         listOfWord = [x for x in listOfWord if x != ' ']

         return listOfWord

     else:

         cutted = jieba.cut(bigString, cut_all=False)

         listOfWord  = []

         for word in cutted:

             if word not in stop_word:

                 listOfWord.append(word)

         return [word.encode('utf-8') for word in listOfWord]

 '''

     交叉训练

 '''

 CLASS_AD        = 1

 CLASS_NOT_AD    = 0

 def testClassify():

     listADDoc = []

     listNotADDoc = []

     listAllDoc = []

     listClasses = []

     print "----loading document list----"

     #两千个标注为广告的文档

     for i in range(1, 1001):

         wordList = textParse(open('subject/subject_ad/%d.txt' % i).read())

         listAllDoc.append(wordList)

         listClasses.append(CLASS_AD)

     #两千个标注为非广告的文档

     for i in range(1, 1001):

         wordList = textParse(open('subject/subject_notad/%d.txt' % i).read())

         listAllDoc.append(wordList)

         listClasses.append(CLASS_NOT_AD)

     print "----creating vocab list----"

     #构建词袋模型

     listVocab = createVocabList(listAllDoc)

     docNum = len(listAllDoc)

     testSetNum  = int(docNum * 0.1);

     trainingIndexSet = range(docNum)   # 建立与所有文档等长的空数据集（索引）

     testSet = []                       # 空测试集

     # 随机索引，用作测试集, 同时将随机的索引从训练集中剔除

     for i in range(testSetNum):

         randIndex = int(random.uniform(0, len(trainingIndexSet)))

         testSet.append(trainingIndexSet[randIndex])

         del(trainingIndexSet[randIndex])

     trainMatrix = []

     trainClasses = []

     for docIndex in trainingIndexSet:

         trainMatrix.append(bagOfWords2VecMN(listVocab, listAllDoc[docIndex]))

         trainClasses.append(listClasses[docIndex])

     print "----traning begin----"

     pADV, pNotADV, pClassAD = trainNaiveBayes(array(trainMatrix), array(trainClasses))

     print "----traning complete----"

     print "pADV:", pADV

     print "pNotADV:", pNotADV

     print "pClassAD:", pClassAD

     print "ad: %d, not ad:%d" % (CLASS_AD, CLASS_NOT_AD)

     args = dict()

     args['pADV'] = pADV

     args['pNotADV'] = pNotADV

     args['pClassAD'] = pClassAD

     fw = open("args.pkl", "wb")

     pickle.dump(args, fw, 2)

     fw.close()

     fw = open("vocab.pkl", "wb")

     pickle.dump(listVocab, fw, 2)

     fw.close()

     errorCount = 0

     for docIndex in testSet:

         vecWord = bagOfWords2VecMN(listVocab, listAllDoc[docIndex])

         if classifyNaiveBayes(array(vecWord), pADV, pNotADV, pClassAD) != listClasses[docIndex]:

             errorCount += 1

             doc = ' '.join(listAllDoc[docIndex])

             print "classfication error", doc.decode('utf-8', "ignore").encode('gbk')

     print 'the error rate is: ', float(errorCount) / len(testSet)

 # 分类方法(这边只做二类处理)

 def classifyNaiveBayes(vec2Classify, pADVec, pNotADVec, pClass1):

     pIsAD = sum(vec2Classify * pADVec) + log(pClass1)    #element-wise mult

     pIsNotAD = sum(vec2Classify * pNotADVec) + log(1.0 - pClass1)

     if pIsAD > pIsNotAD:

         return CLASS_AD

     else:

         return CLASS_NOT_AD

 '''

     训练

     params:

         tranMatrix 由测试文档转化成的词空间向量 所组成的 测试矩阵

         tranClasses 上述测试文档对应的分类标签

 '''

 def trainNaiveBayes(trainMatrix, trainClasses):

     numTrainDocs = len(trainMatrix)

     numWords = len(trainMatrix[0]) #计算矩阵列数, 等于每个向量的维数

     numIsAD  = len(filter(lambda x: x == CLASS_AD, trainClasses))

     pClassAD = numIsAD / float(numTrainDocs)

     pADNum = ones(numWords); pNotADNum = ones(numWords)

     pADDenom = 2.0; pNotADDenom = 2.0

     for i in range(numTrainDocs):

         if trainClasses[i] == CLASS_AD:

             pADNum += trainMatrix[i]

             pADDenom += sum(trainMatrix[i])

         else:

             pNotADNum += trainMatrix[i]

             pNotADDenom += sum(trainMatrix[i])

     pADVect = log(pADNum / pADDenom)

     pNotADVect = log(pNotADNum / pNotADDenom)

     return pADVect, pNotADVect, pClassAD

 '''

     将输入转化为向量，其所在空间维度为 len(listVocab)

     params:

         listVocab-词集

         inputSet-分词后的文本，存储于set

 '''

 def bagOfWords2VecMN(listVocab, inputSet):

     returnVec = [0]*len(listVocab)

     for word in inputSet:

         if word in listVocab:

             returnVec[listVocab.index(word)] += 1

     return returnVec

 '''

     读取保存的模型，做分类操作

 '''

 def adClassify(text):

     fr = open("args.pkl", "rb")

     args = pickle.load(fr)

     pADV        = args['pADV']

     pNotADV     = args['pNotADV']

     pClassAD    = args['pClassAD']

     fr.close()

     fr = open("vocab.pkl", "rb")

     listVocab = pickle.load(fr)

     fr.close()

     if len(listVocab) == 0:

         print "got no args"

         return

     text = textParse(text, False)

     vecWord = bagOfWords2VecMN(listVocab, text)

     class_type = classifyNaiveBayes(array(vecWord), pADV, pNotADV, pClassAD)

     print "classfication type:%d" % class_type

 if __name__ == "__main__":

     loadStopword()

     while True:

         opcode = raw_input("input 1 for training, 2 for ad classify: ")

         if opcode.strip() == "":

             begtime = time.time()

             testClassify()

             print "cost time total:", time.time() - begtime

         else:

             text = raw_input("input the text:")

             adClassify(text)

代码测试效果：

1、训练。

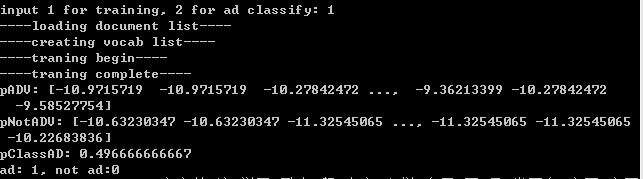
2、实例测试。

分类为1则归为广告，0为普通文本。

p.s.

此分类器的准确率，其实是比较依赖于训练语料的，机器学习算法就和纯洁的小孩一样，取决于其成长（训练）条件，“吃的是草挤的是奶”，但，“不是所有的牛奶，都叫特仑苏”。